運動量の法則とは別に角運動量の法則が出てきたんだけど、よくわかんない…


考え方は運動量の法則とよく似ているから、ベクトルの向きに注意して考えるのが大事だね。
今回は角流体力学の運動量の法則について解説します。
結構、回転の分野は苦手な方も多いと思いますので、基礎の部分から説明していこうと思います。
ベクトルの外積

ベクトルの外積のについて簡単にだけ復習しておきます。
表記は掛け算記号であらわされ、具体的には下図のように成分計算できます。
ベクトル\(\textbf{a}\)と\(\textbf{b}\)の外積である\(\textbf{a×b}\)の向きですが、下図のように\(\textbf{a}\)から\(\textbf{b}\)へ右手を巻き付かせる方向で、右ねじの向きになります。
次に、\(\textbf{a×b}\)の大きさ\(|\textbf{a×b}|\)ですが、これは\(\textbf{a}\)と\(\textbf{b}\)が張る平行四辺形の面積に相当します。
式的には\(\textbf{a}\)と\(\textbf{b}\)がなす角をθとすると、
\[|\textbf{a×b}|=|\textbf{a}||\textbf{b}|sinθ\]
となります。
角運動量って?
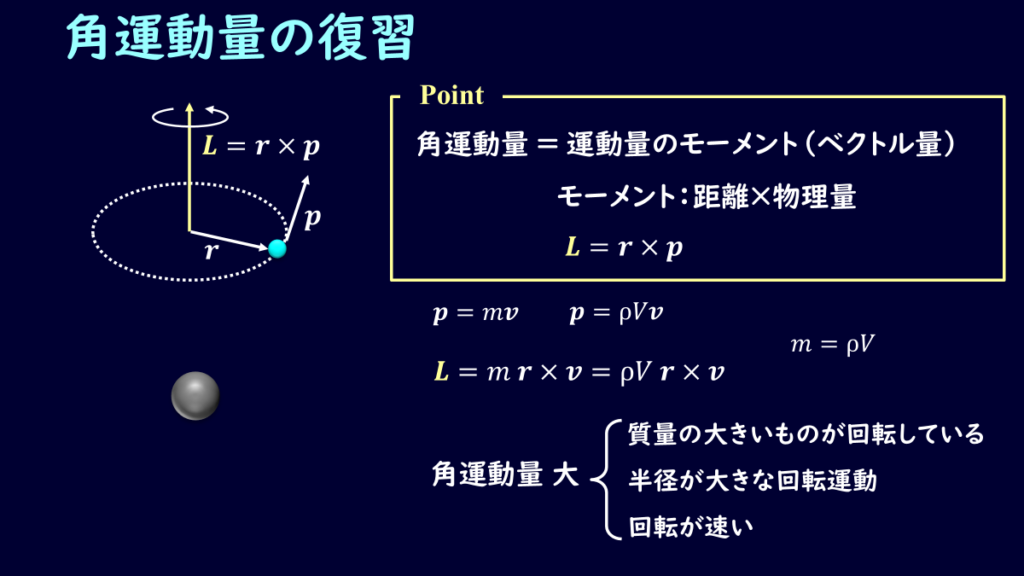
角運動量は運動量のモーメントに相当するもので、モーメントとは、距離×運動量で表される物理量になります。
直感的なイメージとしては、この角運動量が大きいと、速い回転をしている、もしくは半径の大きな円運動をしている、ということになります。
まぁ大きな遠心力を受けそうな運動になっていると考えてもらえればよいかと。
この角運動量はベクトル\(\textbf{L}\)で表され、距離のベクトル\(\textbf{r}\)と運動量のベクトル\(\textbf{p}\)の外積で表されることになります。
よって、
\[\textbf{L}=\textbf{r}×\textbf{p}\]
と書けますので、角運動量のベクトルの向きとしては、\(\textbf{r}\)と\(\textbf{p}\)が作る平面に対して垂直な方向となります。
角運動量ベクトルの方向に対して右ネジの方向に回転運動する、という風に考えるようにしましょう。
角運動量の法則
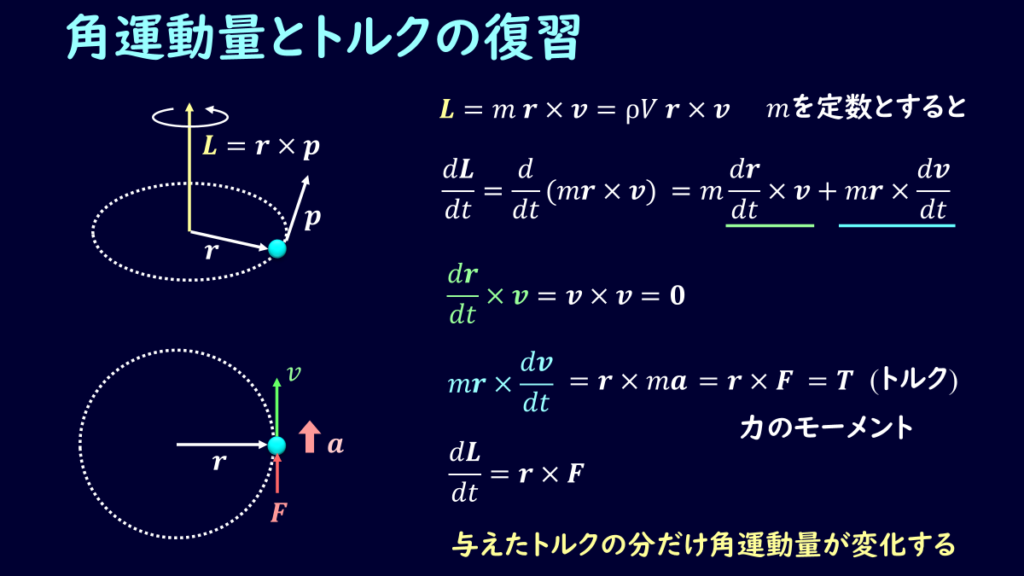
運動量の法則と同様に、下記のような法則が成立します。
\[\textbf{r×F}=\frac{d}{dt}\textbf{r×p}\]
これは質点系の力学の話でも同様で、流体力学で取り扱う流体素片にも対象範囲を広げているわけですね。
運動量の法則は、与える力を\(F\)、力を与えている時間を\(Δt\)、運動量変化を\(ΔM\)とすると、
\[FΔt=ΔM\]
あるいは、
\[F=\frac{d}{dt}mv\]
でしたので、両辺をモーメントで考えているだけで中身は非常によく似ていることがわかります。
角運動量の法則は与えた力のモーメントの分だけ、角運動量が増えたり減ったりしますよ、ということを言っているわけですね。
別の表記として、左辺の\(\textbf{r×F}\)はトルク\(\textbf{T}\)で表すことができ、右辺は角運動量\(\textbf{L}\)を使って表せば、
\[\textbf{T}=\frac{d\textbf{L}}{dt}\]
と書き表わすことができます。
簡単な例題 曲がった流管
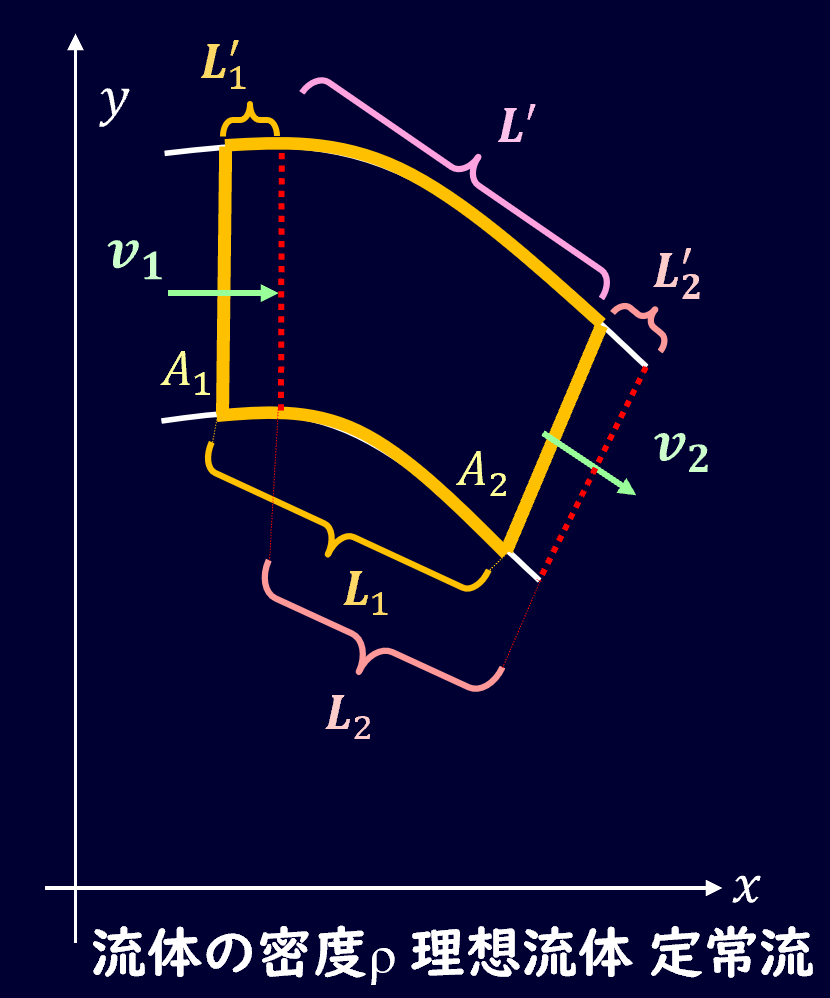
それでは曲がった流管に対して、角運動量の法則を適用して、どれくらいのトルクがかかるかを調べてみましょう。
考え方は運動量の法則のときと同じで、検査領域を考えることからスタートしましょう。
図のようにオレンジ枠の部分を検査領域として設定して、\(Δt\)秒後に赤の点線部に移動したとします。
オレンジ枠の部分の角運動量を\(\textbf{L}_1\)、赤枠部分の運動量を\(\textbf{L}_2\)とすると、これらの差分をとることで、共通している部分を消去することになります。
余った部分をそれぞれ\(\textbf{L}'_1\)、\(\textbf{L}'_2\)とすると、
\[\textbf{T}Δt=\textbf{L}'_2-\textbf{L}'_1\]
と書きあらわすことができます。
次に\(\textbf{L}'_1\)や\(\textbf{L}'_2\)を考えていきましょう。
これらの角運動量を持つ流体要素の位置ベクトルを\(\textbf{r}_1\)、\(\textbf{r}_2\)とし、それぞれの断面積を\(A_1、A_2\)、流速を\(\textbf{v}_1、\textbf{v}_2\)とします。
図のように、速度ベクトルと位置ベクトルは直角になっているわけではないので、なす角をそれぞれ\(θ_1、θ_2\)とします。
このように設定すると、角運動量\(\textbf{L}'_1\)、\(\textbf{L}'_2\)は
\[\textbf{L}'_1=ρV_1\textbf{r}_1×\textbf{v}_1cosθ_1\]
\[\textbf{L}'_2=ρV_2\textbf{r}_2×\textbf{v}_2cosθ_2\]
ここで、それぞれの体積を\(V_1、V_2\)としています。
この体積はそれぞれ
\[V_1=A_1v_1Δt\]
\[V_2=A_2v_2Δt\]
と書きあらわすことができ、体積流量を\(Q\)とすると、連続の式から
\[Q=A_1v_1=A_2v_2\]
なので、
\[\textbf{L}'_1=ρQΔt\textbf{r}_1×\textbf{v}_1cosθ_1\]
\[\textbf{L}'_2=ρQΔt\textbf{r}_2×\textbf{v}_2cosθ_2\]
となります。
単位時間で考えると\(Δt\)を消去することができるので、
\[\textbf{L}'_1=ρQ\textbf{r}_1×\textbf{v}_1cosθ_1\]
\[\textbf{L}'_2=ρQ\textbf{r}_2×\textbf{v}_2cosθ_2\]
となり、差をとると、
\[\textbf{L}'_2-\textbf{L}'_1=ρQ(\textbf{r}_2×\textbf{v}_2cosθ_2-\textbf{r}_1×\textbf{v}_1cosθ_1)\]
と書くことができます。
大きさを考えると、\(\textbf{r}_1\)と\(\textbf{v}_1cosθ_1\)のなす角は直角なので、\(\textbf{L}'_1\)の大きさは\(|\textbf{r}_1||\textbf{v}_1|cosθ_1\)となります。
同様に、\(\textbf{L}'_2\)の大きさは\(|\textbf{r}_2||\textbf{v}_2|cosθ_2\)と書けますね。
\(\textbf{r}_1、\textbf{r}_2、\textbf{v}_1、\textbf{v}_2\)の大きさをそれぞれ\(r_1、r_2、v_1、v_2\)すると、
流管に発生するトルクの大きさは、
\[|\textbf{T}|=|\textbf{L}'_2|-|\textbf{L}'_1|=ρQ(r_2v_2cosθ_2-r_1v_1cosθ_1)\]
と書きあらわすことができます。
まとめ
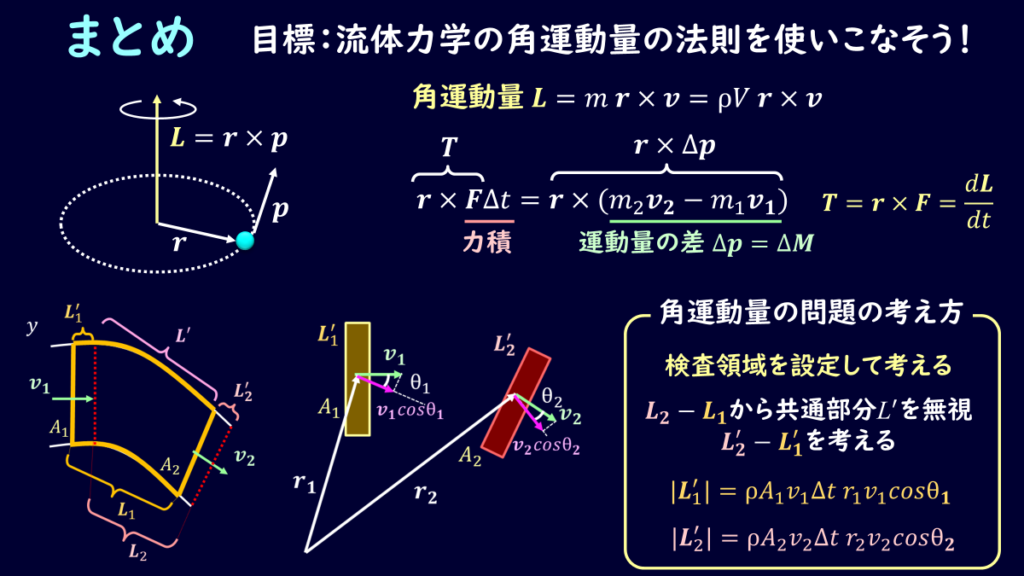
流体力学の角運動量の法則について解説しました。
角運動量の分野は苦手な方も多いかと思いますが、運動量の法則と流れは同じですので、図形的な部分をしっかりと理解しておきましょう。
