推力っていうのが新たに出てきたんだけど、これって何なの?


ジェット機とかの動力になる力だね。流体力学の運動量の法則で説明できるから解説するね。
今日は推力について解説します。
作用反作用の法則、運動量の法則を使えば理解できる内容ですので、問題をしっかりと解いて自分のものにしていきましょう。
推力って?
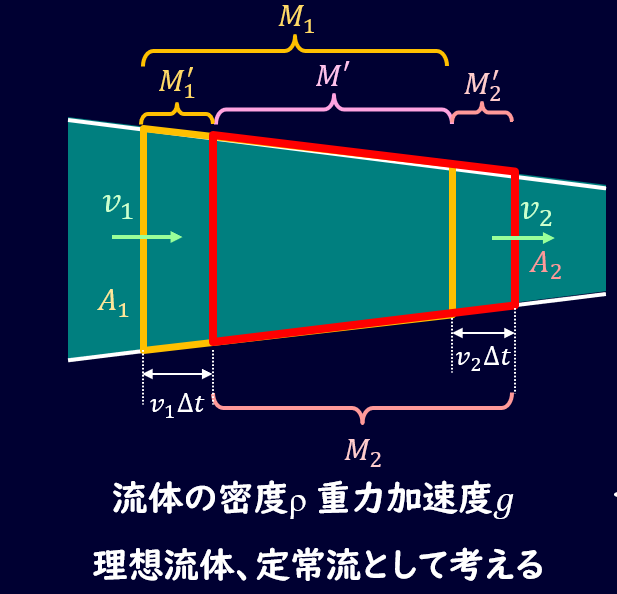
1番簡単な例でいきましょう。
これまでやってきた断面積が変化する流管を考えます。
この問題は過去に詳しく取り扱っていますので、詳細な解説はそちらを参考にしていただければと思います。
検査領域を図のように設定すると、運動量の法則から、
\[F=ρQ_2v_2-ρQ_1v_1\]
となりますが、この力を分解した時に、流管に作用する力が出てくるのでした。
重力などの体積力を無視し、表面力を\(f_s\)、反力を\(f\)とすると、
\[F=f_s+f=p_1A_1-p_2A_2+f\]
となります。
\(F\)は先ほど運動量の法則で求まっていますので、反力を求めると、
\[f=ρQ_2v_2-ρQ_1v_1-p_1A_1+p_2A_2\]
となります。
仮にこの断面積が変化する流管が下図のような状態になっているとしましょう。
出口側は流体が吹き出している状態、左側はなんらかの力で流体を押し出している状態となっています。
こうすると流体が吹き出たことによって、流管は反力を受け、吹き出た方向と逆向きに力を受け運動することになりますね。
このときの反力を推力、英語でスラストと呼びます。
ロケットとかガンダムとか好きな人は『スラスター』と呼ばれる動力を発生させる装置の名前を聞いたことがあるかもしれませんね。
なんかガスみたいなのが吹き出してロケットとか動いているのを見たことある人も多いと思います。
タンクの推力
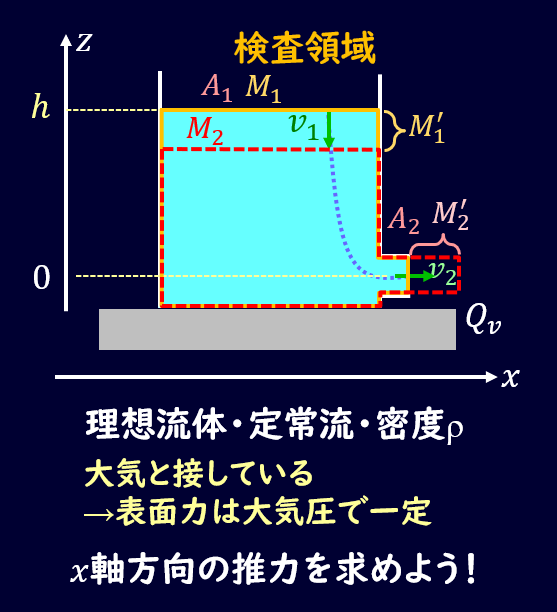
それではもう少し具体的な問題を扱っていきましょう。
トリチェリの定理で扱ったタンクオリフィスについてです。
図のようなタンクを考え、検査領域を設定します。
流体は密度ρの理想流体、重力加速度を\(g\)としておきます。
まず、タンクから出てくる流体の速度\(v_2\)はトリチェリの定理から求まって、
\[v_2=\sqrt{2gh}\]
となります。\(h\)はタンク内の液面の高さです。
運動量の法則はベクトルで考えるので、推力として発生する\(x\)軸方向の運動量や力を考えるだけでOKです。
まぁつまり\(y\)軸方向の力や運動量を考えても推力に関係ないので、無視しておきます、ということです。
ということで\(x\)軸方向の運動量の法則を考えると、タンクから出てくる流量を\(Q_2\)として、
\[F_x=ρQ_2v_2\]
となります。
タンクの吹き出し口の断面積を\(A_2\)とすると、
\[F_x=ρA_2v_2^2=2ρA_2v_2gh\]
と計算できます。
推力はこの流体に作用する力の作用反作用から求まるので、推力\(f\)は
\[f=-F_x=-2ρA_2v_2gh\]
シャワーヘッドの推力
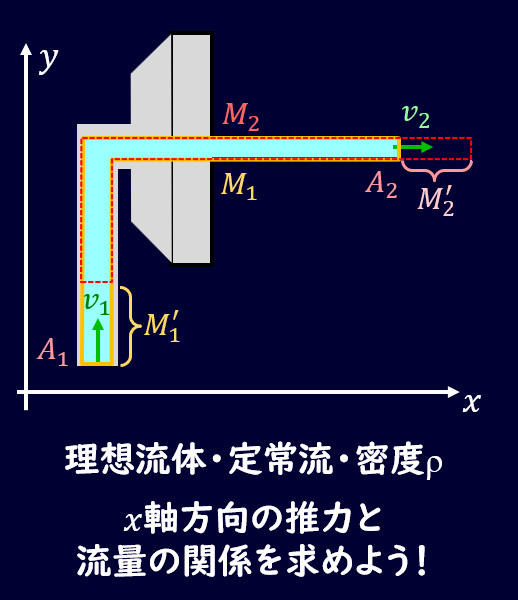
これはあまり推力と呼ばないかもしれませんが、身近な例の鉄板の問題なので解説しておきます。
シャワーの水を出しすぎてヘッドが暴れてビシャビシャになってしまったことがあるのではないでしょうか?
ということでシャワーの水が吹き出たときに、シャワーヘッドにかかる力を求めてみましょう。
シャワーヘッドを図のように設定します。
ホースの中を通過する速度を\(v_1\)、吹き出た流体の流速を\(v_2\)とします。
ここでも流体は密度ρの理想流体とします。
\(x\)方向、\(y\)方向の運動量の法則を考えると、
\[F_x=ρQv_2\]
\[F_y=-ρQv_1\]
となります。
ホースの断面積を\(A_1\)、シャワーの吹き出し口の断面積を\(A_2\)とすると、
\[F_x=ρ\frac{Q^2}{A_2}\]
\[F_y=ρ\frac{Q^2}{A_1}\]
と書き表わすことができ、流量の2乗で力が発生することになります。
ジェットエンジンの推力
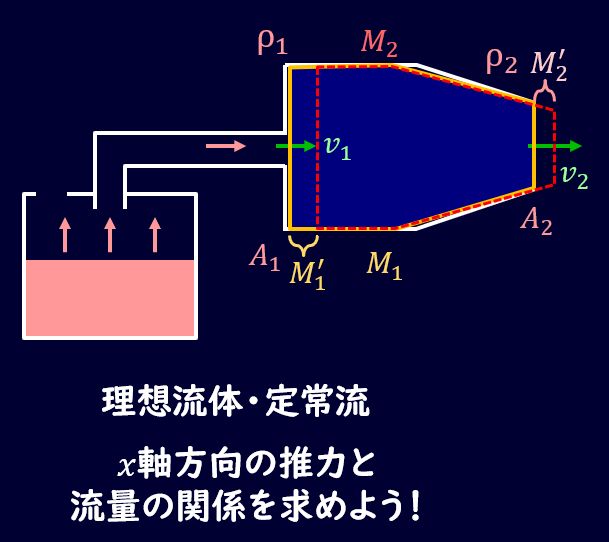
すごく雑な図で説明します。燃料を空気と混ぜて燃やすことで、流体の密度が高くなり、噴出口から噴き出る形になります。
外にある空気と混ぜることになるので、入り口は大気圧、出口側も大気に噴出するので大気圧になります。
ポイントになるのは、流体の密度が変化するところですね。
これらの前提を踏まえた上で、運動量の法則を適用してみましょう。
運動量の法則を使うと、
\[M'_2-M'_1=ρ_2A_2v_2Δt×v_2-ρ_1A_1v_1Δt×v_1\]
単位時間あたりに変換して、連続の式を用いると、
\[A_1v_1Δt=A_2v_2Δt=Q_V\]
ここで\(Q_V\)は体積流量です。
よって、
\[F=ρ_2Q_Vv_2-ρ_1Q_Vv_1\]
表面力は大気圧で一定なので、推力\(f\)は\(F\)の反作用となり、
\[f=-F=-(ρ_2Q_Vv_2-ρ_1Q_Vv_1)\]
と求めることができます。
密度が変化する場合でも、運動量の法則を用いると推力を求めることができます。
まとめ
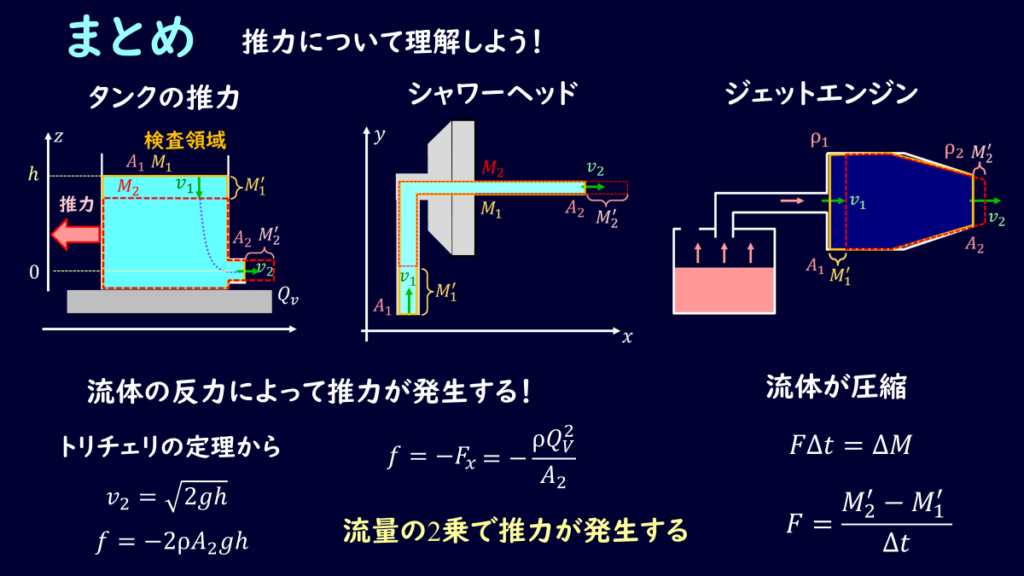
推力について解説しました。
運動量の法則と作用反作用の法則をしっかりと使いこなせれば理解できると思いますので、流れをしっかりと把握しておきましょう。
