壁に流体をぶち当ててるんだけど、これどうやって解くの?


これも運動量の法則を使って解いていけるから解説していくね。
今回もよくある問題、流体を壁に当てた時にどうなるかという問題です。
受ける力や流量がどのようになるか見ていきましょう。
問題設定
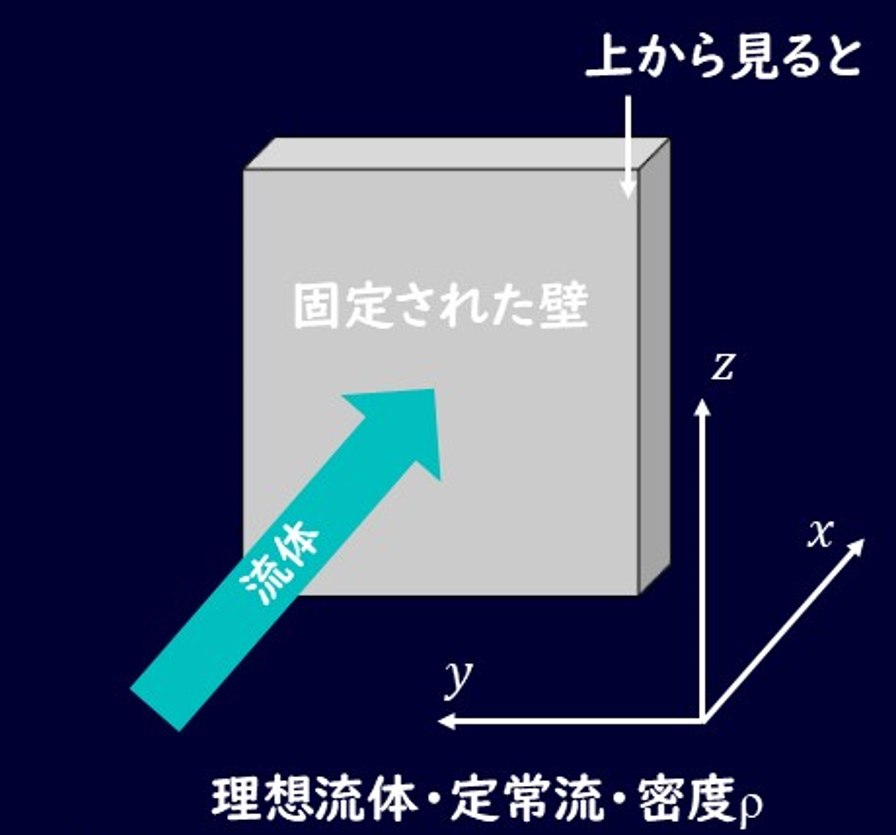
まず、流体は密度ρの理想流体で、壁に当たったときの損失はないとします。
壁に当たった流体は全て壁に沿って流れるとします。
まぁ壁に当たってはねたりしないということです。
では、検査領域を設定しましょう。
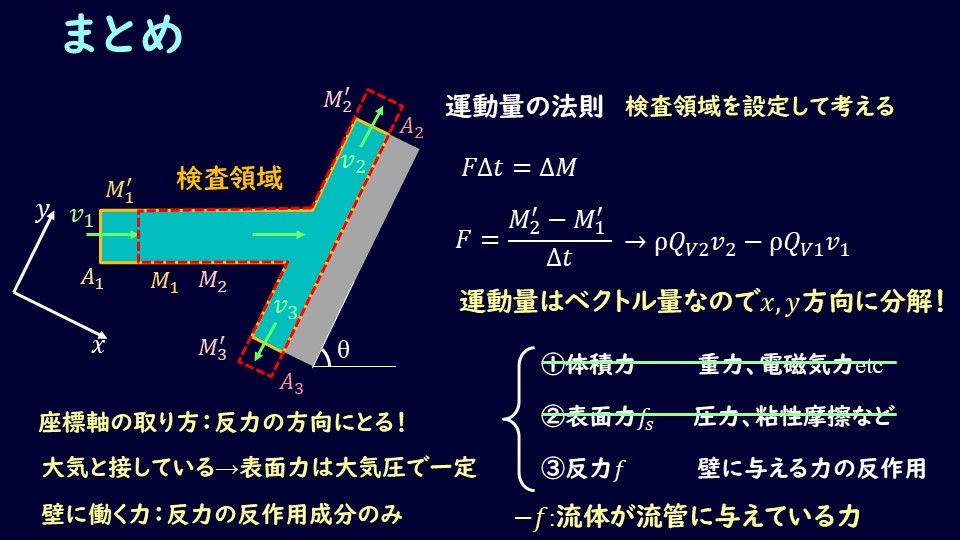
検査領域は上図の状態を上から見たとして、下図のように壁に沿った流体部分を対象とします。
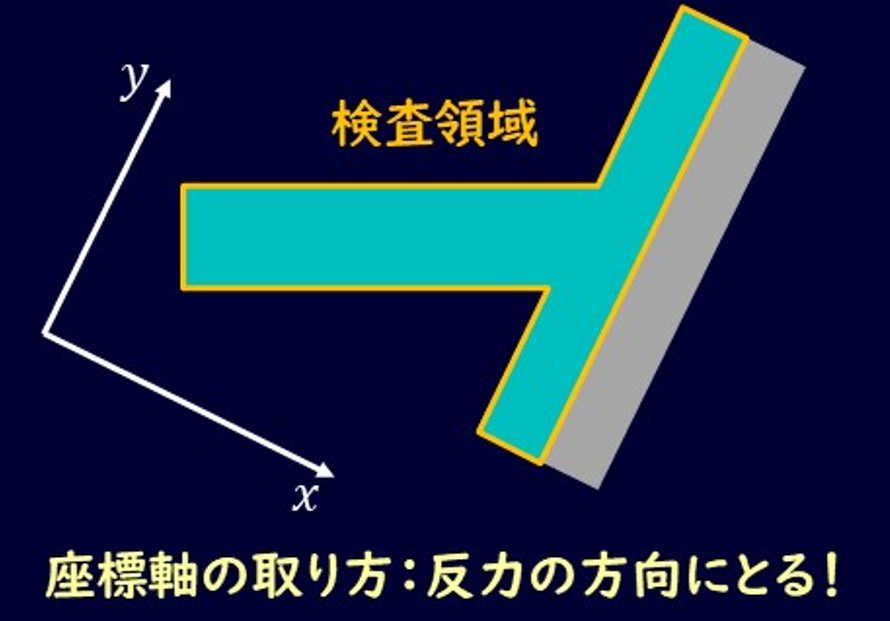
ポイントとしては座標軸は壁からの反力の方向にとるようにしましょう。
このように検査領域を取ると、検査面としては入口側と分岐した後の2つ、合計3つ取りたくなりますね。
取りたくなってください。お願いします。
そうすると、それぞれの面を通る流量を\(Q_1、Q_2、Q_3\)として、連続の式から
\[Q_1=Q_2+Q_3\]
となります。
次にエネルギーの観点を考えると、
圧力はいずれの場所でも大気圧に等しくなるので、平面上で高さが同じとすればベルヌーイの定理から流速も各点で等しくなります。
それぞれの検査面での流速を\(v_1、v_2、v_3\)とすると、
\[v_1=v_2=v_3=v\]
となりますね。
運動量の法則を使う
さて、ここから運動量を考えていきましょう。
運動量はベクトル量なので向きを考える必要がありますね。
今回は先ほど示した図のように板に垂直な方向に\(x\)軸を、板に沿った方向を\(y\)軸を設定します。
さらに入射してきている流体がなす角をθとして、運動量の法則を考えましょう。
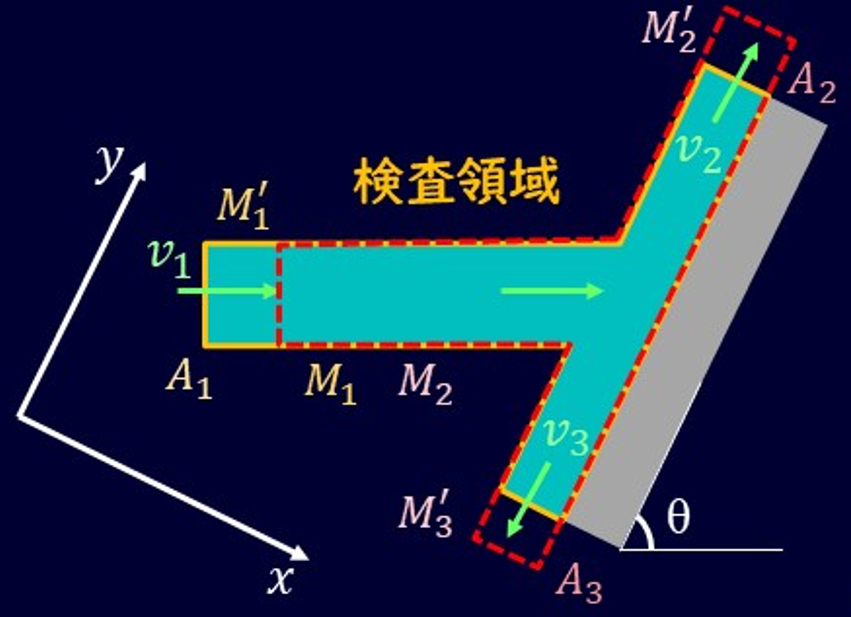
単位時間後に検査領域内の流体が赤枠部に移動したとすると、運動量変化は検査領域と赤枠部が重なっていない部分を考えればよいのでした。
入射側の重なっていない部分の運動量を\(M'_1\)として、まず、\(x\)軸方向の運動量\(M'_{1x}\)を考えると、
\[M'_{1x}=F_xΔt=-ρA_1v_1Δt×vsinθ\]
ここでΔtを単位時間とすると、\(A_1v_1Δt=Q_1\)なので、
\[F_x=-ρQ_1vsinθ\]
となります。
ちなみに出ていく側の\(x\)軸方向の運動量\(M'_{2x}+M'_{3x}\)は、座標系の取り方に注意するとロになりますね。
ということで\(y\)軸方向の運動量を考えましょう。
同じように単位時間あたりの運動量変化を考えると、
\[F_y=(ρQ_2v-ρQ_3v)-ρQ_1vcosθ\]
となります。
検査領域にかかる力が求まったので、体積力、表面力、反力に分解していきましょう。
とは言っても、今回のケースでは重力は考慮しておらず、体積力は考える必要がありません。
表面力についても、圧力は大気圧で一定、さらに理想流体を考えているので摩擦も考慮しなくてよいので、表面力も考えなくてよくなります。
ということで、運動量の法則で求めた力はそのまま反力となります。
ただし、板からの反力は板に垂直に発生するので、\(y\)軸方向の反力はゼロとなります。
よって
\[ρQ_2v-ρQ_3v-ρQ_1vcosθ=0\]
ρと\(v\)で両辺を割ると、
\[Q_2-Q_3-Q_1cosθ=0\]
となります。
連続の式と合わせて、
\[Q_2=\frac{1+cosθ}{2}Q_1\]
\[Q_3=\frac{1-cosθ}{2}Q_1\]
と各方向の流量が求まります。
また、板にかかる力\(f\)は\(F_x\)の反作用の成分となるので、
\[f=ρQ_1vsinθ\]
となります。
移動羽に流体を当てた時
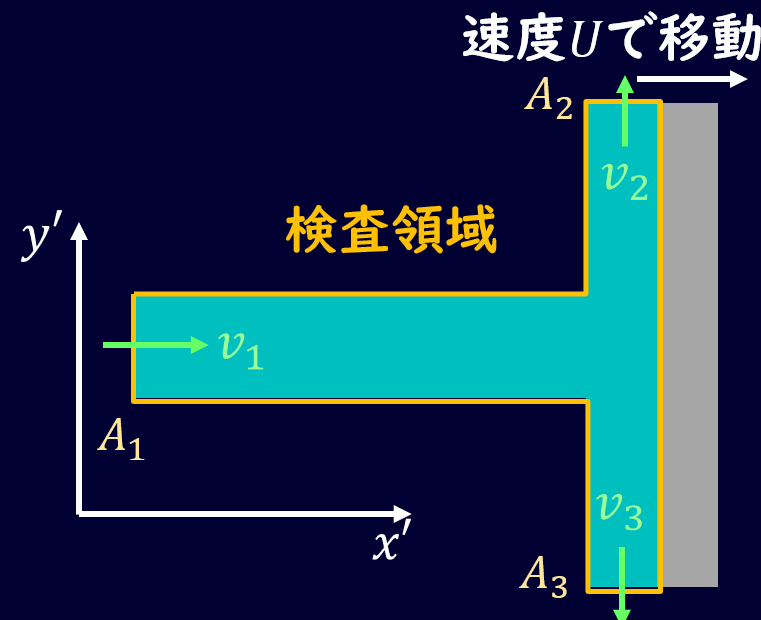
図のような移動羽を考えます。
移動羽は先ほどとは異なり、羽に流体が当たった力で羽が移動するようなものとなります。
この時の運動量の法則を考え、移動羽の移動速度\(U\)と、羽にかかる力\(f\)を考えてみましょう。
ちなみに図の羽の高さは同じ位置にあるとします。
流体が流速\(v\)であたることで羽が移動しますので、羽から流体を見ると、\(v-U\)で流体がぶつかってきているように見えます。
こういう時は相対座標系で考えると考えやすく、羽に乗っかって流体を見るイメージで進めていきましょう。
こうすると固定した板とほぼ同じ扱いをすることができます。
まず、相対座標系で見た羽にぶつかる流体の流速を\(v'\)とすると、
\[v'=v-U\]
となります。
先ほどの固定された板と同じく、ベルヌーイの定理を考え、流体の圧力は大気圧で等しいとすると、位置エネルギーも高さが同じなので等しいので、上側に流れる流体の流速\(v'_2\)と下側に流れる流体の流速\(v'_3\)も入ってくる流体の流速と等しくなります。
よって、
\[v'=v'_2=v'_3\]
となります。
次に連続の式を考えましょう。
流体が入ってくる側の検査面の断面積を\(A_1\)、上側の検査面の断面積を\(A_2\)、下側の検査面の断面積を\(A_3\)とすると、
\[A_1v'=A_2v'+A_3v'\]
となります。
よって
\[A_1=A_2+A_3\]
移動羽の上下が対称な構造で中央に流体が当たっているのであれば、\(A_2=A_3\)となりますので、
\[A_1=2A_2\]
それぞれの検査面の流量を\(Q_1、Q_2、Q_3\)とすると、
\[Q_1=Q_2+Q_3=2Q_2\]
と書き表わすことができます。
ここまでくれば、運動量の法則を使って、流体にかかる力\(F\)を求めにいきましょう。
運動量の法則を使う
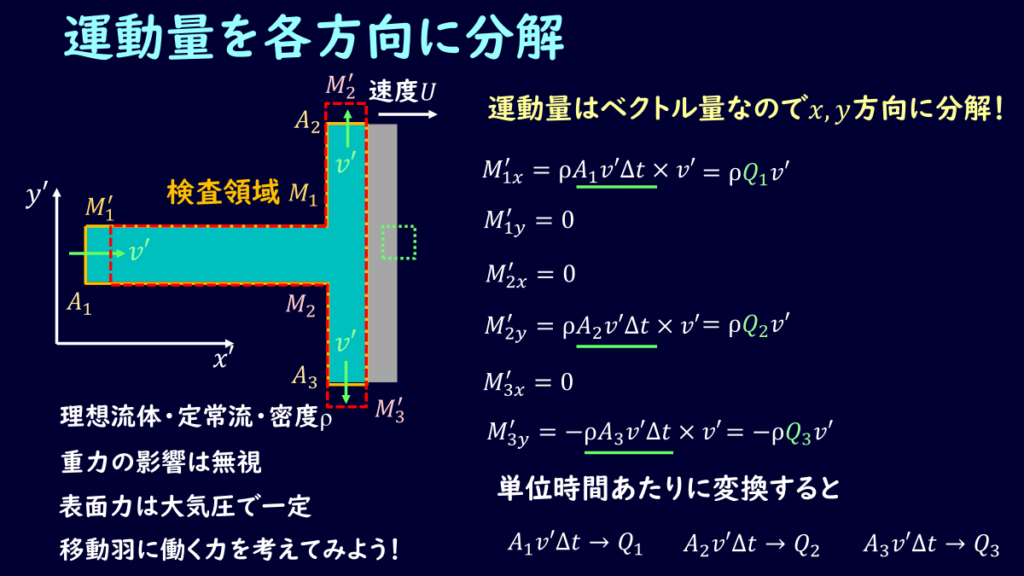
この運動量の法則も相対座標系で考えることにします。
運動量はベクトル量なので、\(x\)軸方向と\(y\)軸方向を考える必要があります。
まず、\(x\)軸方向ですが、羽にぶつかる流体側の考えるべき運動量\(M'_{1x}\)は
\[M'_{1x}=ρQ_1v'\]
となります。
羽に当たったあとの流体側の\(M'_{2x}\)と\(M'_{3x}\)は対称な構造になっているため等しく、
\[M'_{2x}=M'_{3x}=ρQ_2v'\]
となりますね。
よって、\(x\)軸方向の力\(F_x\)は
\[F_x=2M'_{2x}-M'_{1x}=-2ρQ_2v'-ρQ_1v'\]
となります。
次に\(y\)軸方向の運動量ですが、\(M'_{1y}\)はゼロですね。
羽にあたった後の流体の運動量は、\(x\)軸方向と同じように考えることができて、
\[M'_{2y}=-M'_{3y}=ρQ_2v'\]
となりますが、力\(F_y\)を考えると、
\[F_y=M'_{2y}+M'_{3y}-M'_{1y}=0\]
となりますね。
ということで、\(x\)軸方向のみを考えればよくなります。
運動量の法則で求めた力を分解していくわけですが、先ほどの固定板のときと同じく、圧力は大気圧で一定になるので、反力だけを考えればよくなります。
よって反力\(f\)は、
\[f=F_x=-ρQ_1v'=-ρQ_1v'\]
となります。
この反力の反作用が流体による羽に作用する力なので、
\[-f=ρQ_1v'=ρQ_1(v-U)\]
と求めることができます。
まとめ
板に流体を当てたときの運動量の法則について解説しました。
今までの知識を総動員すれば問題なく解けますので流れをしっかりと理解しましょう。
