ピトー管って一体なんなの?普通のマノメーターと何か違うの?


ピトー管はよどみ点を利用して圧力を測定できるものになっていて、マノメーターとは少し扱いが違うよ。
今回はピトー管についてです。
このピトー管もベルヌーイの定理を使うことで、流速などがわかるようなものになっています。
ピトー管の理解に必要な静圧、動圧、よどみ点についても解説します。
静圧、動圧って?
ベルヌーイの式を見てみましょう。
\[\frac{1}{2}ρv^2+p+ρgz=一定\]
単位体積あたりのエネルギー保存の法則を示しているわけですが、圧力項が入っていることに注目しましょう。
そう、エネルギーなのですが、圧力という側面も持っていることになるんですね。
ということでベルヌーイの定理の各項を分類します。
運動エネルギーの項を動圧、圧力の項を静圧と呼び、動圧と静圧の和を全圧と呼びます。
めっちゃ簡単。
分けたところでなんか意味あんの?


それぞれの圧力を測定できる機器がピトー管なんだ。
ピトー管による測定
よどみ点について
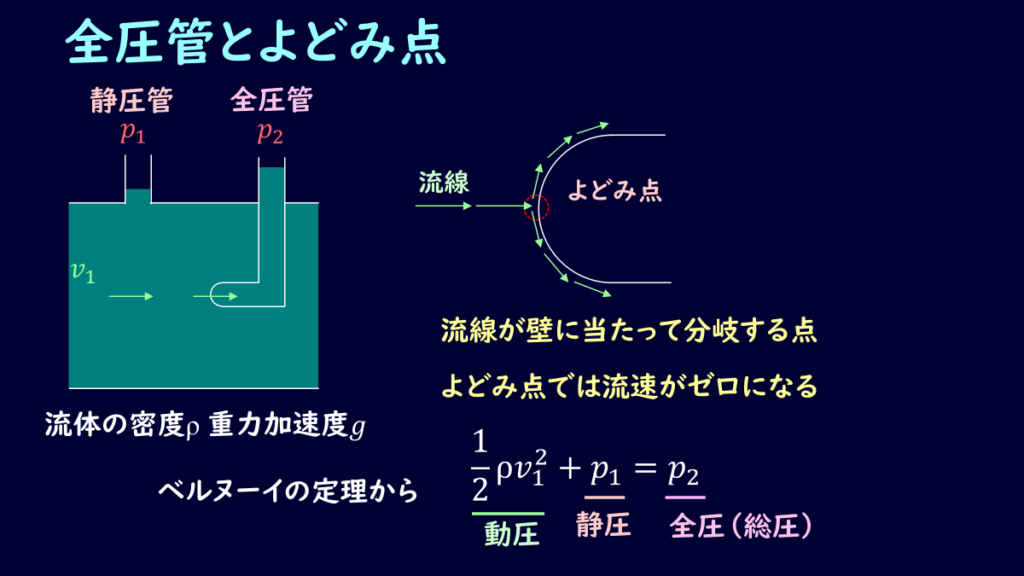
それではピトー管による圧力測定について説明します。
ポイントになるのはよどみ点で、このよどみ点では流速がゼロになり、流線が分岐します。
図に書くとこんな感じですね。
基本的に流線は枝分かれしないのですが、よどみ点では流線が分岐します。
この流速がゼロになることを利用して圧力を測定し、ベルヌーイの定理から全圧を測定することができます。
具体的にはこんな感じの流管を用意します。
一般的には静圧と全圧の両方を測れるような構造になっています。
左側の点における流速、圧力をそれぞれ\(v_1、p_1\)として、ピトー管のよどみ点の圧力を\(p_2\)とすると、ベルヌーイの定理から、
\[\frac{1}{2}ρv_1^2+p_1=p_2\]
となります。
よどみ点側の運動エネルギーはゼロになりますので、よどみ点の圧力\(p_2\)がそのまま全圧になるわけです。
この圧力がピトー管にかかって、管の中の流体を押し上げているような形になるので、ピトー管の液面の高さを測定すると全圧がわかるということになります。
動圧を求める際には、左側のマノメーターの高さを読んで、ピトー管で求めた全圧との差を取れば良く、
\[\frac{1}{2}ρv_1^2=p_2-p_1\]
となります。
この式から速度を求めることができ、
\[v_1=\sqrt{\frac{2(p_2-p_1)}{ρ}}\]
となります。
ちなみに前回のオリフィスやトリチェリの定理の場合と同様に、このピトー管も理論値と実験値を補正する係数があり、ピトー係数\(k\)というものがあります。
このピトー係数を使って実際の速度\(v'_1\)を表すと、
\[v'_1=kv_1=k\sqrt{\frac{2(p_2-p_1)}{ρ}}\]
となります。
まとめ
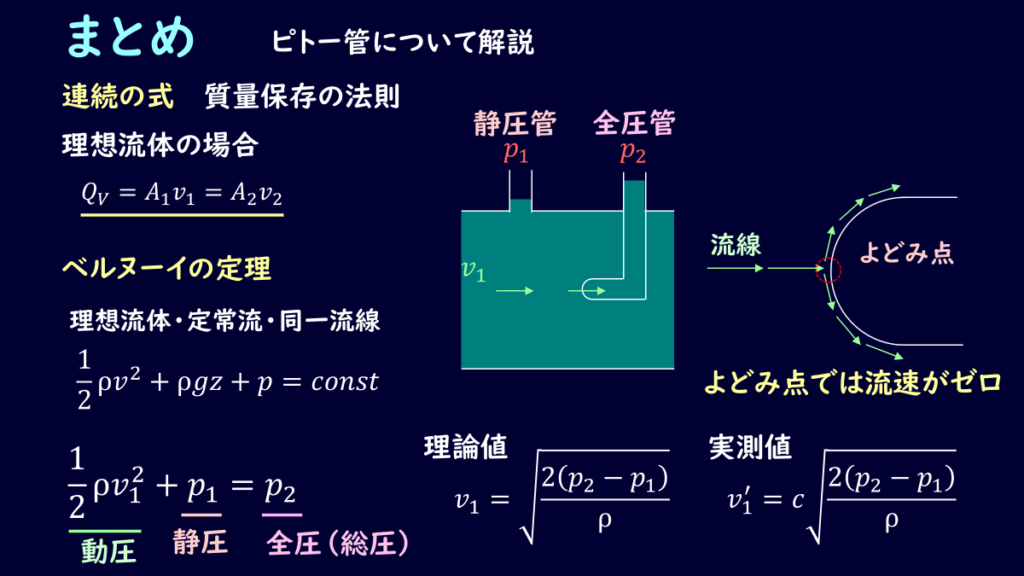
今回はピトー管について解説しました。
静圧、動圧、全圧、よどみ点をしっかり理解して、ベルヌーイの定理を使えば、測定原理も理解できると思いますので、しっかりと自分の頭の中でイメージできるようにしましょう。
