オリフィスってなんなの?


壁に穴を開けたような、絞りの機構の一種だね。流量の調整や測定に使ったりするよ。
今回はベルヌーイの定理の応用例としてオリフィスについて解説します。
オリフィスは壁に穴が空いたような構造になっており、流量制御など幅広く応用されているものになっています。
ベルヌーイの定理は過去の記事で解説していますので参考にしていただければと思います。
オリフィス
先ほども少し出ましたが、端的に言うと壁に空いた穴です。
その穴を流体が通ったときの流体の挙動を利用して、流量制御とか色んなことができるのです。
加工が簡単なため、工業的によく使われます。
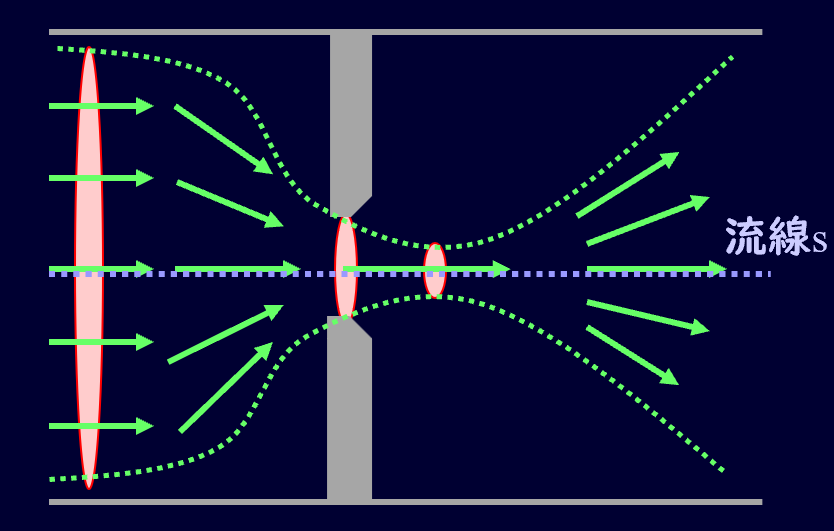
オリフィスで押さえておかなければいけないポイントは縮流です。
縮流がどういったものかを押さえて、どのように流量を制御したり測定しているのかを理解しておきましょう。
縮流って?
ということで縮流について解説します。
オリフィスは流れを穴で絞るような構造になっていて、その穴を通ってきた流体は図のような流れ方をします。
ここでポイントになるのが、オリフィスが設置されている角の剥離部分と、穴を通った後に流速ベクトルが1番密になる箇所がある部分です。
前者の角の部分については、流体が流れていると慣性によって角の部分まで流体が行き届かず、流体が剥離するような現象が起こります。
この辺りは後の講義で取り扱う内容なので、今はそうなんだくらいで思っていただいてOKです。
後者の流速ベクトルが1番密になる部分ですが、この流れのことを縮流とよびます。
縮流部分のベルヌーイの式

さて、それではベルヌーイの式を適応していきましょう。
オリフィスの左側の断面積、流速、圧力を\(A_1、v_1、p_1\)とし、オリフィスの穴の部分の断面積、流速、圧力を\(A_2、v_2、p_2\)とし、縮流部分の断面積、流速、圧力を\(A_3、v_3、p_3\)とします。
まず連続の式から、
\[A_1v_1=A_2v_2=A_3v_3\]
となります。
ベルヌーイの式は
\[\frac{1}{2}ρv^2_1+p_1=\frac{1}{2}ρv^2_2+p_2=\frac{1}{2}ρv^2_3+p_3\]
これらを使って\(v_3\)を求めにいきます。
で、どのパラメータを使って\(v_3\)を表すかですが、圧力については\(p_1\)と\(p_3\)はマノメーターをつけることで簡単に測定できますので、これらを使っていきます。
一方、オリフィスの穴部分の圧力は測定が難しいので、\(p_2\)は使わないようにします。
そうすると、ベルヌーイの式から、
\[v_3^2-v_1^2=\frac{2(p_1-p_3)}{ρ}\]
次に連続の式を使って\(v_1\)を変形します。
ここでは管の面積である\(A_1\)と縮流部分の面積\(A_3\)を使います。
そうすると、
\[v_3^2-v_1^2=v_3^2\left(1-\frac{A_3^2}{A_1^2}\right)\]
となり、
\[v_3=\sqrt{\frac{2(p_1-p_3)}{ρ\left(1-\frac{A_3^2}{A_1^2}\right)}}\]
と求まります。
なんかものごっつい式になったね…


そうだね。ここから少し近似を入れてわかりやすくしていこう。
トリチェリの定理でも使った近似を使って式を整理していきます。
どういう近似だったかというと、入り口の管の面積は穴の大きさに比べて十分に大きいという条件を使う近似でしたね?
現在の式で見えている断面積の2乗の比を下記のように変形します。
\[\frac{A_3^2}{A_1^2}=\frac{A_2^2}{A_1^2}\frac{A_3^2}{A_2^2}\]
こうすると、\(A_1>>A_2\)なので、ここの項をゼロに近似できます。
つまり、
\[v_3=\sqrt{\frac{2(p_1-p_3)}{ρ}}\]
となります。
これはトリチェリの定理の時の式と同じですね。
実際のオリフィスの流量
さて、オリフィスを通過したあとの理想的な場合の流量\(Q\)は
\[Q=A_3v_3=A_3\sqrt{\frac{2(p_1-p_3)}{ρ}}\]
と、面積をかけることで求めることができます。
しかし、流体に粘性があると、エネルギーをロスし、流速が小さくなり、縮流部分に流れ込んでくる流量も小さくなります。
ということで、実際には補正係数をかけて、実測値に合わせます。
流速に関する補正係数を\(C_v\)とし、縮流部分の実際の流速を\(v'_3\)とすると、
\[v'_3=C_vv_3=C_v\sqrt{\frac{2(p_1-p_3)}{ρ}}\]
となります。
流量に関しても同様で、補正係数をαとして実測値に合わせます。
このαには名前がついていて、流量係数という名前がついており、実測値の流量を\(Q'_v\)とすると、
\[Q'_v=αQ_v=αA_2\sqrt{\frac{2(p_1-p_3)}{ρ}}\]
あれ?面積が\(A_2\)に変わっているけど…


そう、面積の部分もαの中に入れ込んで、オリフィスの穴の径という定数になるようにしているんだ。
縮流部分の面積は流速などによって変化するので、流速などが変わっても変化しないオリフィスの穴の大きさをつかいます。
じゃあ流量係数αの中身ってどうなっているの?と疑問に思うかもしれませんが、ここは実験的に求めていきます。
なので、このオリフィスだったらこの流量係数、というようにあらかじめ流量測定して決めておくのです。
オリフィスの流量係数はおおよそ0.6くらいになることが多いです。
ちなみにこの流量係数は前回の記事のトリチェリの定理にも出てきたりはしますが、値や式の中身は問題設定によって変わってきますので気をつけていただければと思います。
縮流が起こらないようにするには?
オリフィスは作るのが簡単ではあるものの、縮流によってエネルギーロスが発生してしまいます。
ではエネルギーロスを少なくするにはどうすれば良いかですが、そもそも壁の部分で急激に開口面積が変化してしまっていることが問題なので、ここを改善してあげればよい話になります。
流れが入ってくる側を図のように丸くした構造をノズルと呼びます。
これはオリフィスよりは聞いたことがある人が多いのではないでしょうか。
さらに出入り口の開口面積を徐々に小さくするような構造をペンチュリ管と呼んでいます。
ペンチュリ管はオリフィスに比べて加工が難しく、コストがかかってしまうデメリットがありますが、縮流が発生しづらい構造になっているのが特徴です。
まとめ
オリフィスについて解説しました。
縮流が起こることで流量係数の使い方に少し注意する点がありますので、しっかりと導出を理解しておきましょう。
