ベルヌーイの定理ってよく出てくるけどよくわからないんだけど…


ベルヌーイの定理は流体力学でも非常にメジャーな定理だから知っている人も多いと思うよ。中身は流体力学におけるエネルギー保存則で、すごく大事な位置づけなのでしっかりと理解できるように解説するね。
本記事はベルヌーイの定理について解説します。
流体力学におけるエネルギー保存則で、いろんなところで使われますので、しっかりと基本的な部分をマスターしておきましょう。
動画での解説はこちら。
ベルヌーイの定理
ベルヌーイの定理は下記のように書くことができます。
\[\frac{1}{2}ρv^2+ρgz+p=一定\tag{1}\]
これがエネルギー保存の法則につながっているわけですが、導出を見ていただいて理解していただきましょう。
微小領域のエネルギーを考える
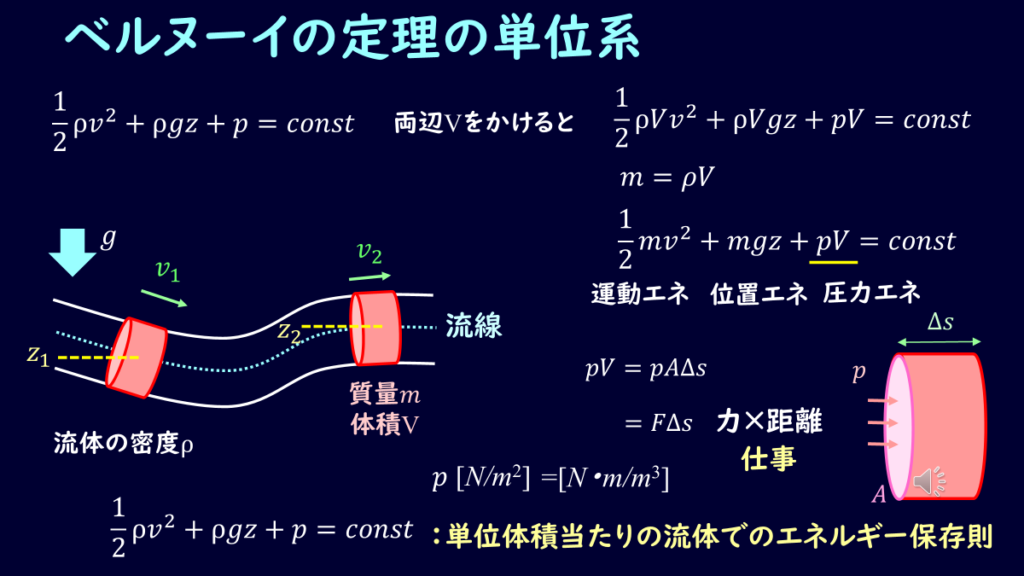
流管を流れる流体のエネルギーを考えてみましょう。
とある体積\(V\)の流体の質量を\(m\)、流速を\(v\)、重力加速度を\(g\)、位置エネルギー\(U\)、運動エネルギー\(T\)を考えます。
単位体積あたりの位置エネルギーは
\[U=\frac{mgz}{V}\tag{2}\]
運動エネルギーは
\[T=\frac{1}{2V}mv^2\tag{3}\]
となります。\(m=ρV\)なので、
\[U=ρgz\tag{4}\]
\[T=\frac{1}{2}ρv^2\tag{5}\]
となり、ベルヌーイの式の第1項、第2項がでてきましたね。
問題になるのは第3項の\(p\)ですね。
単位がそもそも\(Pa\)だったら圧力がエネルギーになるのっておかしいんじゃない?


実は\(Pa=N/m^2\)という単位を変形すると、\(N・m/m^3\)で、単位体積あたりのエネルギーになるんだ。
はい、というわけで、このエネルギー保存の式の中に圧力の項が存在しても問題はなさそうだということがわかります。
では、もう少し深掘りをして、この圧力項が必須であることを理解していきましょう。
圧力は単位面積あたりの力ですので、なんとなく仕事とつながっていると想像できますね。
ちなみにとある経路sに沿って、\(s_1\)から\(s_2\)まで、力\(F\)で物体を移動させたときの仕事\(W\)は
\[W=\int_{s_1}^{s_2} F ds\tag{6}\]
と表すことができます。
圧力と単位体積の仕事
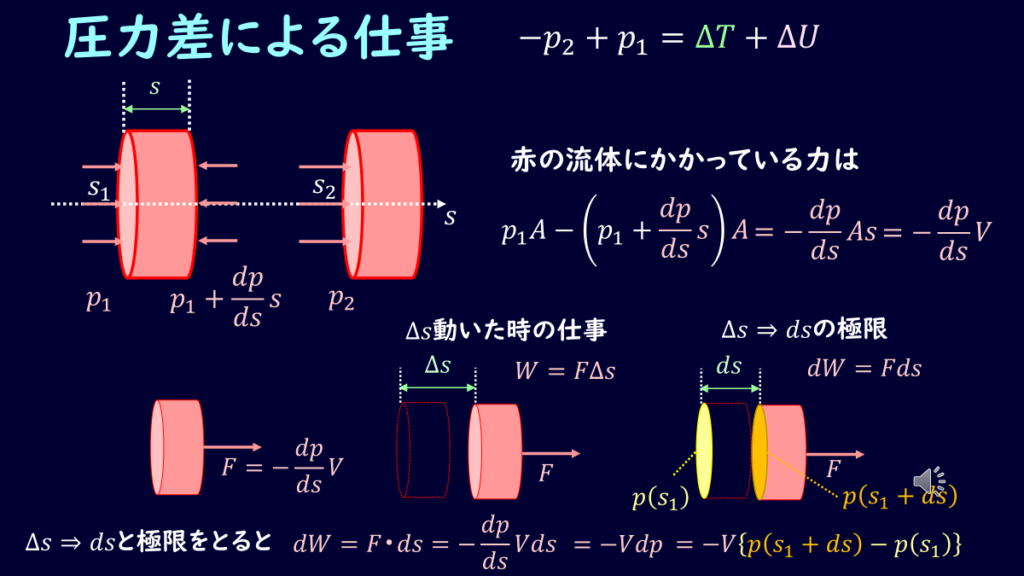
この式を元に微小領域にかかっている圧力を考えましょう。
ちなみにベルヌーイの式は同一流線で成り立つ式ですので、圧力を考える際、面積は流線に垂直な面で考えます。
微小領域の流線に垂直な面\(A\)にかかっている力\(F\)は
\[F=pA-(p+\frac{\partial p}{\partial s}s)A\tag{7}\]
式を整理すると、
\[F=-\frac{\partial p}{\partial s}V\tag{8}\]
となります。
ここで、\(A×s=V\)と体積\(V\)を使用しています。
仕事は
\[dW=-\int^{s_2}_{s_1} \frac{\partial p}{\partial s}Vds\tag{9}\]
と書くことができます。よって、
\[W=-V\int^{p_2}_{p_1} dp\tag{10}\]
となって、
\[W=V(p_1-p_2)\tag{11}\]
となります。
仕事をしたときの物体のエネルギー変化は、運動エネルギーと位置エネルギーの変化をそれぞれ\(ΔT、ΔU\)とすると、仕事の原理から
\[W=ΔT+ΔU\tag{12}\]
と書けて、
\[ΔT=\frac{1}{2}m(v^2_2-v^2_1)\tag{13}\]
\[ΔU=mg(z_2-z_1)\tag{14}\]
となり、仕事の原理と一致します。
オイラーの運動方程式からの導出
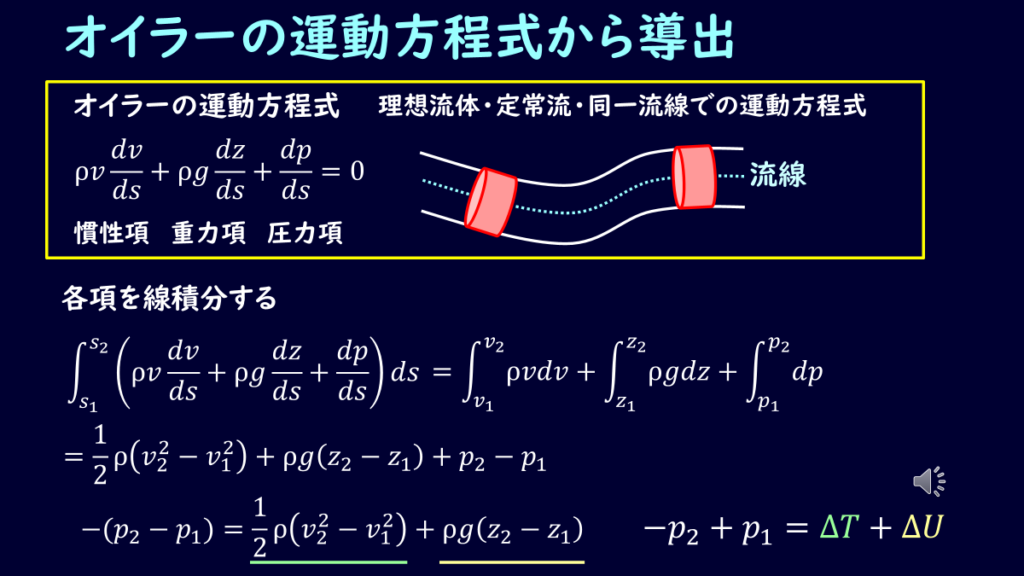
実はベルヌーイの式はオイラーの運動方程式を不定積分することで求めることができます。
積分できる人は結構一瞬で機械的に求まるので、頭に入れておくと便利かもしれません。
オイラーの運動方程式は
\[ρ\frac{dv}{ds}v+ρg \frac{dz}{ds}+\frac{dp}{ds}=0\tag{15}\]
と書けます。
この各項を線積分すると上図のようにベルヌーイの式を導出することができます。
ヘッドについて
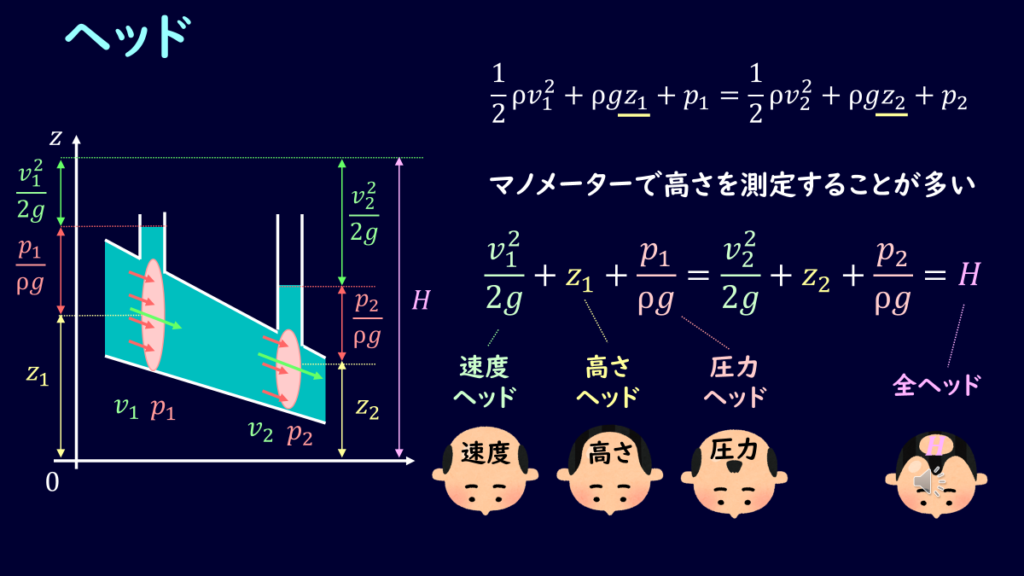
ベルヌーイの定理を少し変形して、ヘッドという概念を導入します。
ヘッドって言うとカッコいいんですが、要するに高さです。
流体静力学の中で、圧力を測るための機器として、マノメーターというものを学習しましたが、
あれは水面の高さを見ることによって圧力を測定することができる機器でしたね。
そう、高さが重要なのです。
今、考えている流体は流れがあり、動いているわけで、単純に圧力や重力だけの成分だけでなく、運動エネルギーの成分も考えないといけないのです。
そこでベルヌーイの定理を使って、高さを見ることで運動エネルギー成分とかを議論するわけですね。
ただ、これまで学んできたベルヌーイの式の各項の単位は、単位体積あたりのエネルギーだったので、各項を高さの単位に変換することを考えていきます。
1番わかりやすいのは重力の項\(ρgz\)ですね。
\(ρg\)で割ることで、高さ\(z\)だけにすることができます。
各項の単位は同じなので、運動エネルギーの項も圧力の項も\(ρg\)で割ることで高さの単位にすることができます。
運動エネルギーの項は、
\[\frac{1}{2g}v^2\tag{16}\]
圧力の項は
\[\frac{p}{ρg}\tag{17}\]
となりますね。
これらの和が一定なので、その定数を\(H\)とすると、
\[\frac{1}{2g}v^2+z+\frac{p}{ρg}=H\tag{18}\]
となります。
それぞれ高さを示していて、第1項を速度ヘッド、第2項を高さヘッド、第3項を圧力ヘッドと言います。
損失を加味する
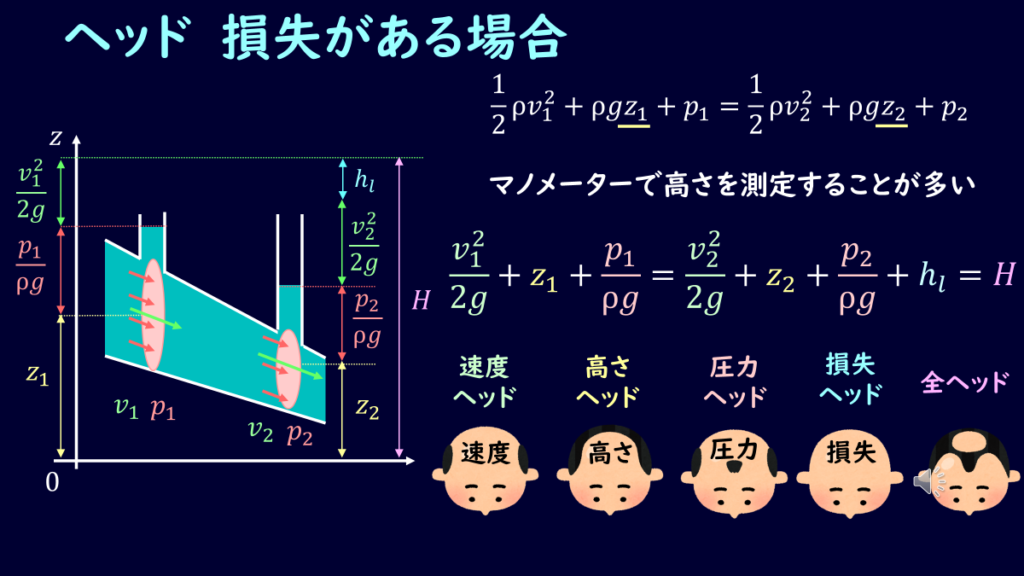
さて、これまで理想流体を取り扱ってきたので、摩擦や粘性などを考慮してきませんでした。
しかし、現実の流体には少なからず摩擦や粘性というものが存在します。
高校物理の力学でも習ったかもしれませんが、摩擦などがあると、力学的エネルギー保存則が成立しなくなります。
これは摩擦によって熱エネルギーなどの力学的なエネルギーとは別のエネルギーが生じ、系から出ていってしまうからですね。
流体力学でも同じことが起こります。
なので現実の流体にベルヌーイの定理を適応させると、摩擦などの損失によるズレが生じます。
この損失を損失項という形でベルヌーイの式に盛り込み、より現実に即した計算ができるようにしていきます。
損失項を\(h_l\)(損失ヘッド)とすると、損失を考慮したベルヌーイの式は
\[\frac{1}{2g}v^2+z+\frac{p}{ρg}+h_l=H\tag{19}\]
となります。
まとめ
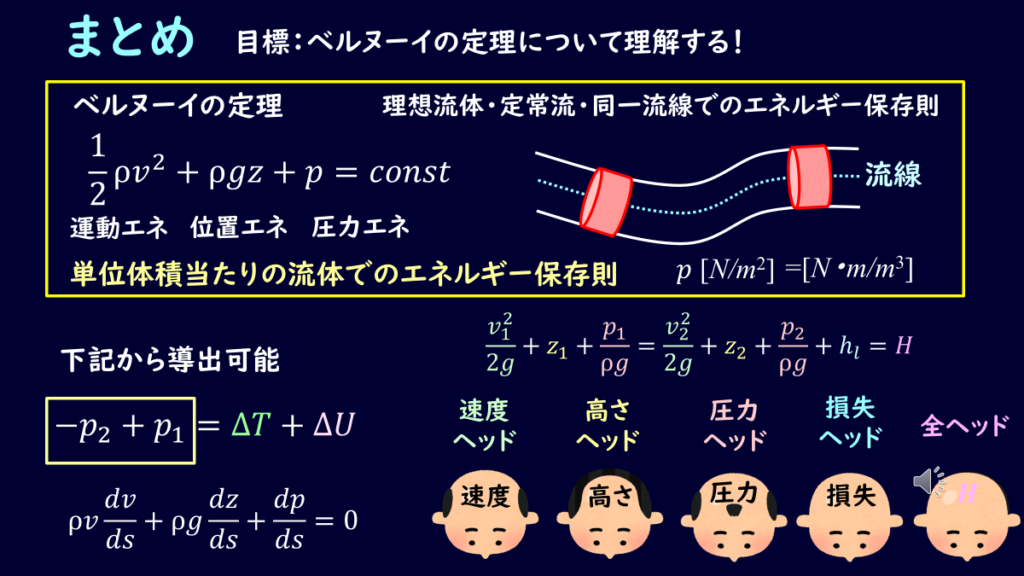
ベルヌーイの定理について解説しました。
流体力学でのエネルギー保存の法則を示しており、ヘッドという概念がよく使われますので、しっかりと理解しておきましょう。
具体的に使っていくのは次回以降の記事で、いろんな演習問題を解いていこうと思いますので、そちらで慣れていっていただければと思います。
