流体の運動方程式でオイラーの運動方程式が出てきたんだけど、何なの?この複雑な形…


ニュートンの運動方程式に比べると複雑な形をしているけど、それぞれの項の意味を理解していけば大丈夫だよ。
今回は流体の運動方程式であるオイラーの運動方程式について解説していきます。
見た目はかなり複雑な形していて、わからなくなってしまう人も多いと思いますが、ひとつひとつ項の意味を理解していくことが1番の近道ですので、がんばっていきましょう。
動画での解説はこちら。
オイラーの運動方程式の形
それではそんな複雑なオイラーの運動方程式を見ていきましょう。
\[ρ\frac{dv}{ds}v+ρg \frac{dz}{ds}+\frac{dp}{ds}=0\]
うん、確かに複雑。
首都圏の地下鉄くらい複雑ですね。
初見では絶対理解できない、Google先生に案内してもらわないと迷う奴です。
オイラーの運動方程式の中身

さて、中身をじっくり見ていくと、項が3つありますね。
それぞれ、慣性項、重力項、圧力勾配項と呼ばれます。
また、オイラーの運動方程式が成り立つのは、理想流体、定常流、同一流線内、という3つの条件が必要ですので、頭の中に入れておきましょう。
粘性が入ってくると、もうひとつの支配方程式であるナビエストークスの運動方程式を使わないといけなくなります。
オイラーの運動方程式の導出
このオイラーの運動方程式を理解するには導出過程を理解することが手っ取り早いので、導出過程を丁寧に見ていきましょう。
出発点は運動方程式というくらいなので、ニュートンの運動方程式から出発します。
ニュートンの運動方程式は\(ma=F\)で、質量が\(m\)、加速度が\(a\)、力が\(F\)ですね。
複数の力がかかっていて、左辺に力の項を持ってくると、
\[ma-\sum{F}=0\]
となります。
これらを微小領域で見てみるとどうなるかを考えていきましょう。
流体の加速度
第1項に流体の加速度\(a\)が含まれています。
ここの理解が非常に重要になってきます。
流体の加速度を考える時には、場所的な速度変化と時間的な速度変化の2種類を考える必要があります。
考えやすくするために、下のような途中で管の面積が狭くなっている状態を考えましょう。
流体は理想流体として考えます。
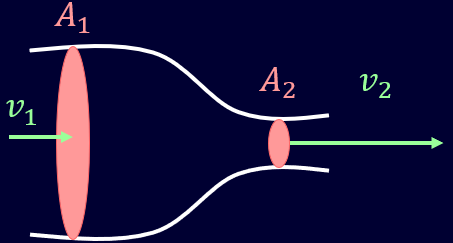
この管に水を流すと、水の速度はどうなるでしょう?
これは前回の講義で解説した通りで、連続の式から狭くなるところで流速は速くなります。
これが定常流で時間的に速度が変化していなければ、管内の流速の測定位置の関係だけで速度が変化していることになります。
これが場所的な速度変化で、移流加速度と言ったりもします。
次に時間的な速度変化ですが、同じような管に徐々に水を流し込む量を増やしていきます。
そうすると同じ測定位置でも時間的に流速が増加していきますね。
このときの加速度が時間的な速度変化で、時間的加速度と呼んだりします。
では、これらが数式的にどのように表されるか見ていきましょう。
位置的な加速度\(a_1\)は
\[a_1=\frac{dv}{dt}\]
と書けますが、この時間微分を位置の微分に直しましょう。すると
\[a_1=\frac{dv}{ds}\frac{ds}{dt}\]
となり、位置の時間微分は速度\(v\)になるので、
\[a_1=\frac{dv}{ds}v\]
と書くことができます。
時間的加速度\(a_2\)は速度の時間微分で表すことができますので
\[a_2=\frac{dv}{dt}\]
となります。
考える加速度は位置的な加速度と時間的な加速度の和となるので、
\[a=a_1+a_2=\frac{dv}{ds}v+\frac{dv}{dt}\]
と書けます。
あれ?時間的加速度があると、時間的に流速がかわるから非定常流になるんじゃ…??


そうだよ。オイラーの運動方程式は定常流という条件がつくから、時間的な速度変化はゼロとして考えるよ。
つまりは今の状況だと、時間的な加速度はゼロになるので、
\[a=a_1=\frac{dv}{ds}v\]
となります。
これはオイラーの運動方程式の第1項の慣性項に相当していますね。
運動方程式の外力を考える
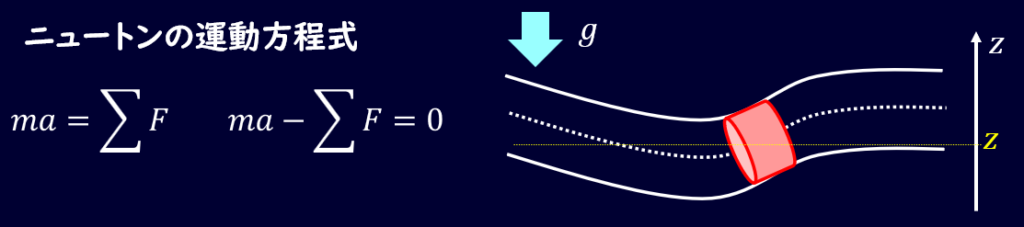
流体にかかっている力を考えるわけですが、流体そのものの重力と流体の圧力の2つが存在しますね。
微小領域を考え、重力と圧力を考えるのですが、オイラーの運動方程式を考える時の重要なポイントがあります。
それは同一流線での運動方程式を立てる、という条件で、この条件があるがゆえに、微小領域も流線に沿った形で考える必要があります。
ということで、流線と\(s\)軸がなす角をθとして微小領域を考えます。
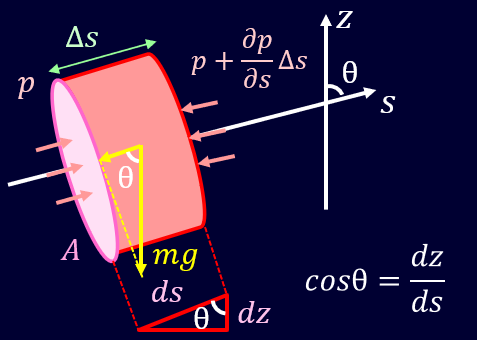
流体の密度をρ、重力加速度を\(g\)、流線と垂直な面積を\(dA\)としますと、
\[dF_g=-ρdAds g cosθ\]
と書けます。
ここで、\(cosθ=\frac{dz}{ds}\)なので、
\[dF_g=-ρdAds g \frac{dz}{ds}\]
となります。
次に圧力です。
圧力は考えている面に対して垂直にかかりますので、
\[dF_p=pdA-(p+\frac{dp}{ds}ds)dA\]
と書けますが、第1項と第2項は消去できて、
\[dF_p=-\frac{dp}{ds}dsdA\]
ニュートンの運動方程式に代入
さて、ここまで求めた式をニュートンの式に代入していきましょう。
\[ma-\sum F=0\]
加速度のところに位置的な加速度を、外力項に重力と圧力の項を入れると、
\[m\frac{dv}{ds}v+ρdAds g \frac{dz}{ds}+\frac{dp}{ds}dsdA=0\]
第1項の\(m\)については密度と体積の掛け算で表せるので
\[ρdV\frac{dv}{ds}v+ρdAds g \frac{dz}{ds}+\frac{dp}{ds}dsdA=0\]
ここで、\(dV=ds×dA\)なので、
\[ρ\frac{dv}{ds}v+ρg \frac{dz}{ds}+\frac{dp}{ds}=0\]
となり、オイラーの運動方程式を導出することができました。
まとめ
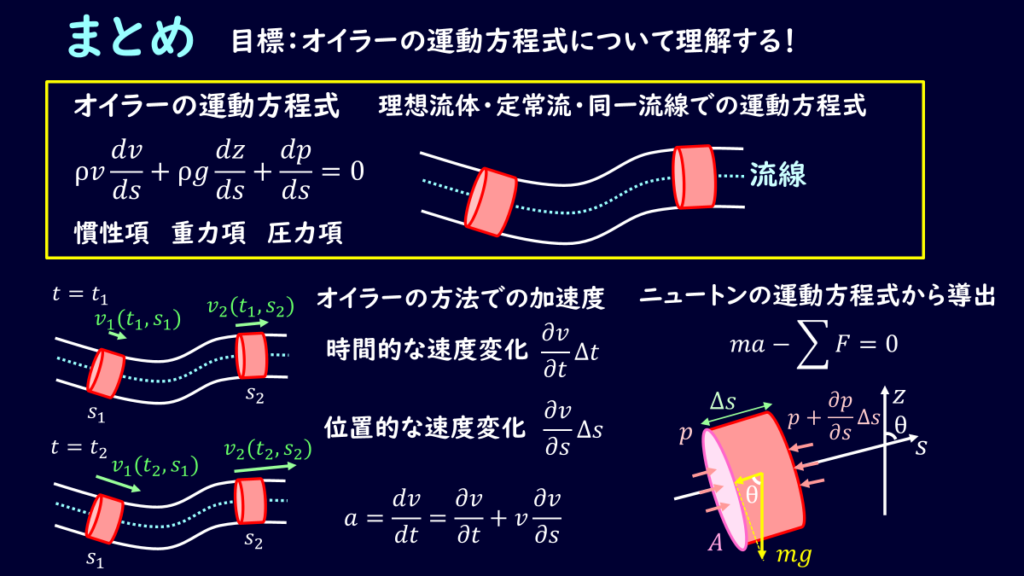
ニュートンの運動方程式を出発点にして、オイラーの運動方程式を導出しました。
導出過程を一度追いかけてみると理解が進むと思いますので、ぜひ一度自分の手を動かしてもらえればと思います。
