03-2.流体力学 流体の連続の式　質量保存の法則

今回は連続の式について解説します。

流体は『流れる物体』です。

この流れという複雑な動きを何かしらの式で表していきたいわけです。

今回はその何かしらの式の中で、高校物理でも扱う『質量保存の法則』を流体力学にもってきて、連続の式を表します。

質点や剛体を取り扱った古典力学でも当たり前のように成り立っていた質量保存の法則。

質量は勝手に消えたり増えたりしない、当たり前と思われるような法則ですが、これが流体力学でどのように扱われるか、見ていきましょう。

復習　流量について

前回の講義で扱った流量のイメージが前提として必要になりますので、しっかりとおさらいしておきましょう。

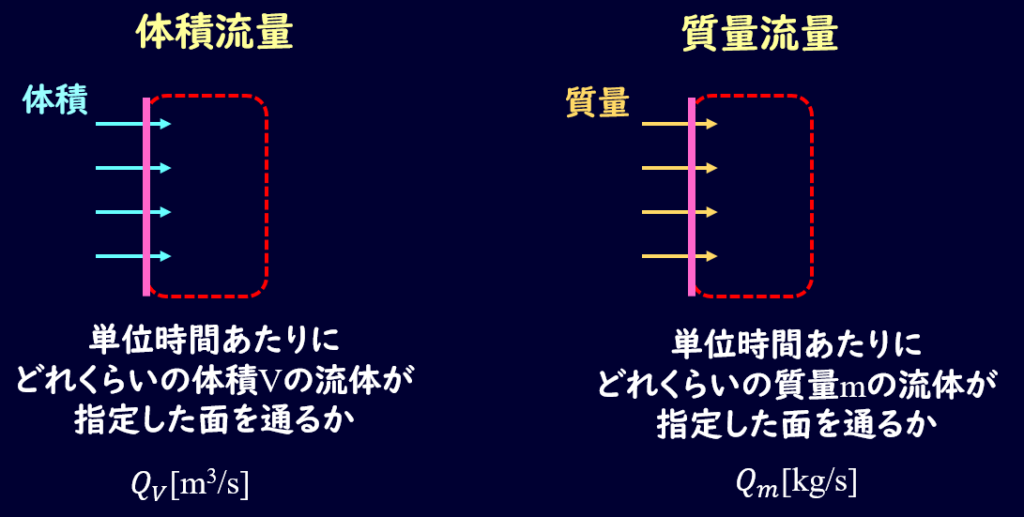
流量はある面積を単位時間にどれくらいの量の流体が通過するかを示した物理量でした。

このどれくらいの量を示すにあたっては重量や質量で表すこともあれば、体積で表すこともあります。

それぞれ質量流量、体積流量という名前がついていましたね。

質量流量の単位は\(kg/sec\)、体積流量の単位は\(m^3/sec\)となっています。

取り扱う流体（理想流体）

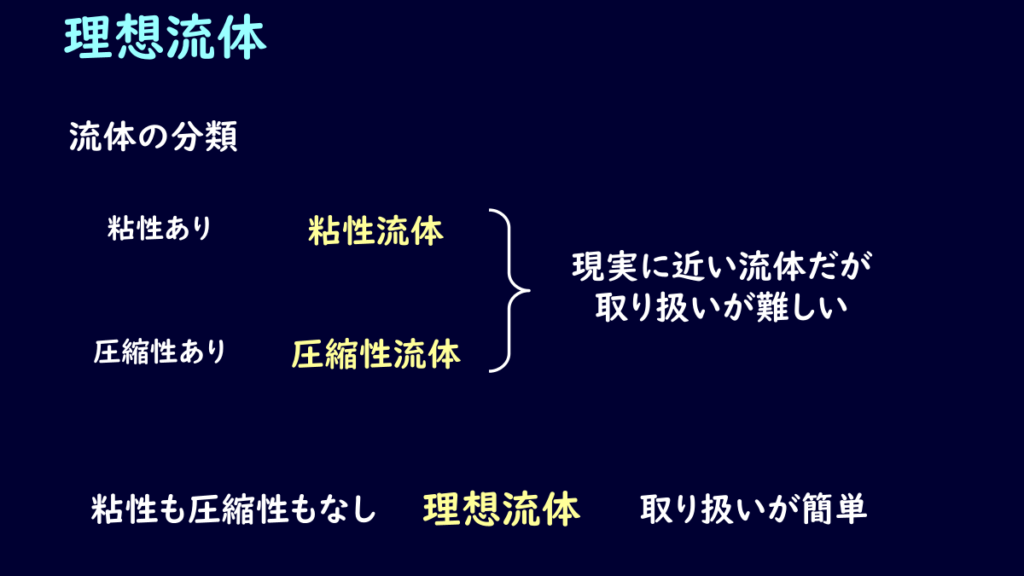
さて、ここで流体の分類についてざっくり説明します。

というのも流体力学を勉強する上で、どういう流体についての運動を考えているか、を理解することは非常に大事です。

粘性の有無、圧縮性の有無っで粘性流体、圧縮性流体という分類がありますが、これらは現実に存在する流体に近いモデルになりますが、取り扱いが複雑になりやすいデメリットがあります。

この取り扱いが難しい部分を簡単にするために、粘性も圧縮性も考慮しない理想流体を導入します。

現実の流体とかけ離れることもありますが、流体力学で起こる簡単な現象を取り扱うのに便利な流体モデルですので、まずはここからスタートしていきたいと思います。

連続の式

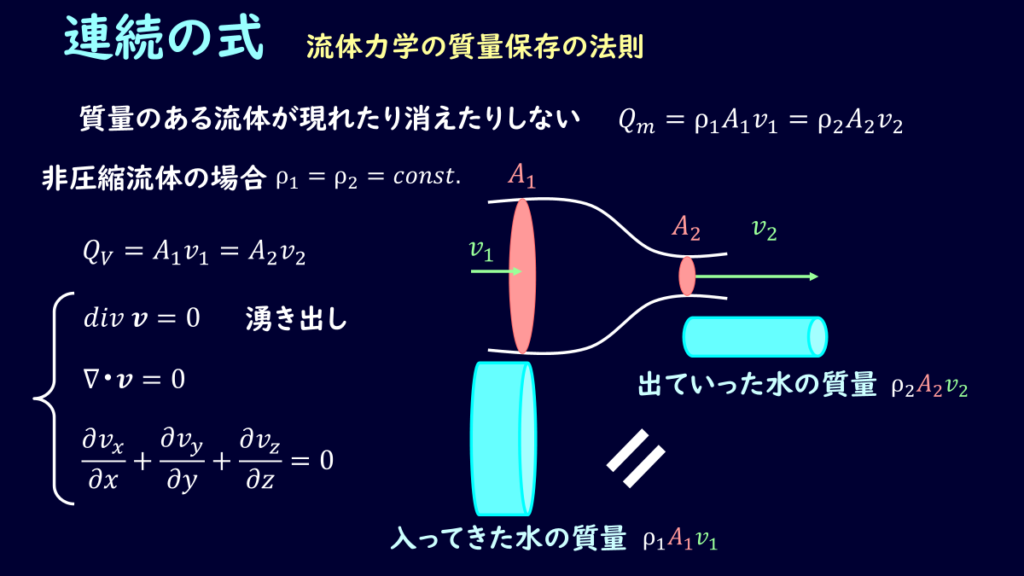
まず、連続の式の形を示しておきます。

実は連続の式の形は色んな表現の仕方があり、混乱される方もいらっしゃるのではと思います。

上図の左側に書いてある４つの式がメジャーですかね。

式の意味しているところは変わらないので、どの表記もしっかりと理解しておくことをおすすめします。

さて、連続の式の説明をする際によく扱われている図として、上図右側のような状態を考えます。

流体が流れている管を考えるのですが、入ってくる側の面の面積を\(A_1\)、流速を\(v_1\)、流体の密度を\(ρ_1\)とし、出ていく側の面の面積を\(A_2\)、流速を\(v_2\)、流体の密度を\(ρ_2\)とします。

質量保存の法則を考えると、入ってきた水の質量と出ていった水の量は一定とならなければいけないので、質量流量を\(Q_m\)とすると

\[Q_m=ρ_1A_1v_1=ρ_2A_2v_2\]

ここで、非圧縮性流体を仮定すると、流体の密度が一定となり、\(ρ_1=ρ_2\)となります。

この時、管を流れる体積流量\(Q_v\)は、

\[Q_v=A_1v_1=A_2v_2\]

となります。

これが連続の式と呼ばれるものになっています。

連続の式の微分形

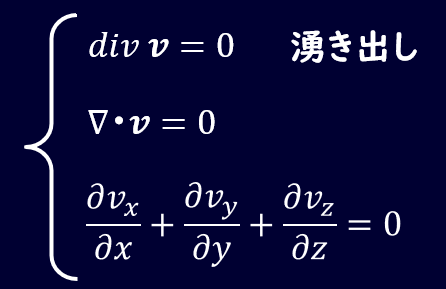
さて、次に連続の式の中で、微分を使って書かれている式について解説していきたいと思います。

大学生の方は先ほどの流量の式を難なく理解できると思いますが、こちらの微分形の方でつまずいている人が多いのではと思います。

まず、divとかかれている数学的な表記ですが、これはdivergence :発散の意味で、∇（ナブラ）と呼ばれる微分演算子との内積を示します。

内積と呼ぶくらいなので、∇はベクトル量になっており、各成分の偏微分記号であらわされます。

\[∇=(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z})\]

ここまでが数学的な話ですが、物理的にどういう意味を持つかを考えていきましょう。

まず、3次元空間で微小な体積を考えます。

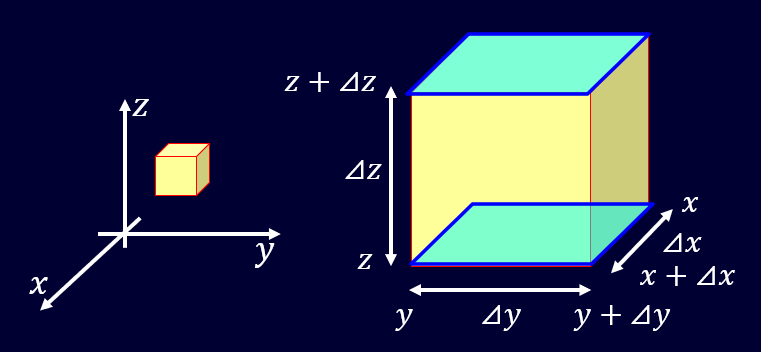
この微小な体積を流速のベクトルがどれくらい通過するか、を考えていきます。

3次元ですので、\(x,y,z\)方向の3方向があり、それぞれの方向の成分がどれだけ通過するか、がポイントになります。

もう一つ大事な前提として、微小面積を通過する際、外向きに貫く成分、すなわち出ていく成分を正として考えますのでご注意ください。

それではまず\(z\)方向に貫く成分を考えましょう。

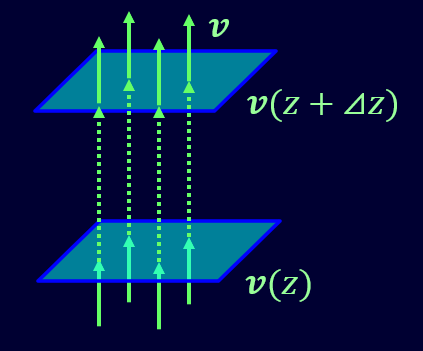
上図のように、微小体積内の\(z\)方向に垂直な面を考え、その面をどれくらいの速度ベクトルが通過するかを考えます。

数式的には下記のように書くことができますね。

\[\boldsymbol{v}(x,y,z+Δz)ΔxΔy-\boldsymbol{v}(x,y,z)ΔxΔy=(\boldsymbol{v}(x,y,z+Δz)-\boldsymbol{v}(x,y,z)ΔxΔy\]

\(ΔxΔy\)は微小領域の青色の面積となっています。

この式を変形して

\[(\boldsymbol{v}(x,y,z+Δz)-\boldsymbol{v}(x,y,z)ΔxΔy=\frac{(\boldsymbol{v}(x,y,z+Δz)-\boldsymbol{v}(x,y,z)}{Δz}ΔxΔyΔy\]

とすると、Δの部分に関して極限をとることで偏微分の形を作り出すことができ、

\[\frac{\partial \boldsymbol{v}(x,y,z)}{\partial z}dV\]

となります。

これを\(x\)方向も\(y\)方向も同様に計算すると、

\[\frac{\partial \boldsymbol{v}(x,y,z)}{\partial x}dV\]

\[\frac{\partial \boldsymbol{v}(x,y,z)}{\partial y}dV\]

という式を得ることができます。

これらは各方向における微小体積を出入りした流体の量の合計となっていますので、和をとってあげると

\[\frac{\partial \boldsymbol{v}(x,y,z)}{\partial x}dV+\frac{\partial \boldsymbol{v}(x,y,z)}{\partial y}dV+\frac{\partial \boldsymbol{v}(x,y,z)}{\partial z}dV=-\frac{\partial ρ}{\partial t}dV\]

となります。

右辺の密度の時間微分は、出入りした分、微小体積からどれだけの密度が変化したかを示しており、これも立派な質量保存の法則になっているわけですね。

両辺を\(dV\)で割り、整理することで

\[(\frac{\partial}{\partial x}+\frac{\partial}{\partial y}+\frac{\partial}{\partial z})\boldsymbol{v}(x,y,z)=-\frac{\partial ρ}{\partial t}\]

となります。

左辺は∇と速度ベクトルの内積になっていますので、

\[∇・\boldsymbol{v}(x,y,z)=div \boldsymbol{v}(x,y,z)=-\frac{\partial ρ}{\partial t}\]

と書けますね。

ここで、理想流体を考えると、非圧縮性流体となりますので、

\[\frac{\partial ρ}{\partial t}=0\]

となって、理想流体のときの連続の式は、

\[∇・\boldsymbol{v}(x,y,z)=div \boldsymbol{v}(x,y,z)=0 \]

となります。

まとめ

流体力学の連続の式について解説しました。

微分形の部分はベクトル解析の分野の内容が出てきて、つまずきやすい部分になっていますので、しっかりとイメージを持てるように理解しておきましょう。