流量ってなんかいろんな表記があるの?ややこしい…


そうだね、流量には体積流量や質量流量といった種類があるね。ちゃんと区別して理解しておかないとこんがらがるから、しっかり解説しておくね。
これまで静止していた流体を取り扱っていましたが、今回から流体が流れる状態を取り扱っていきます。
流体が流れている状態を考えるにあたって、基礎的な用語をある程度知っておく必要がありますので、本記事でしっかりと把握しておきましょう。
そもそも『流れ』とは?
流体が流れている状態というのはどういう物理量を使って表せばよいでしょう?
流体をすごくミクロな範囲で見てみると、流体の流れとは流体の粒子がある速度で動いているように見えます。
その粒子がたくさんあるとして、粒子たちが同じ方向に同じ速度で動いていると、一定の方向に流れ続ける静かな川のような状態になるわけです。
この粒子の動きがみんなバラバラの速度だったりすると、流体の粒子はいろんな方向に動き回ることになるので、静かな川のような状態にはならず、荒れた川のような状態になるわけです。
つまり、流れ方を議論する際に、『流体の速度』、いわゆる『流速』がどのようになっているかを知ることはすごく大事なことになります。
また、今回は流体の粒子までミクロな状態を考えましたが、流体力学では、ある程度の大きさをもった領域を考え、その領域の体積を使ったり、領域内にどの程度の粒子がいるかを密度を使って表すことが多いです。
厳密な議論をする際には領域のサイズを微小領域にまで小さくして、数式化する、といったこともしていくのですが、
そのあたりは後々の講義でまた取り扱いますので、今は『ふーん』くらいでとどめておいていただければと思います。
流れを表す際に『速度』が大事になってくる、という認識をまず持ってもらえればOKです。
流れの見方
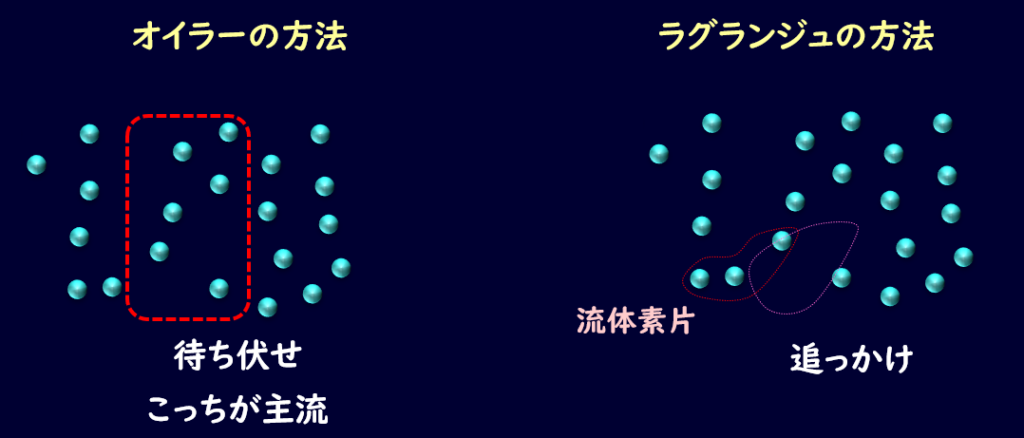
これにはオイラーの方法とラグランジュの方法の2種類があります。
オイラーの方法は待ち伏せ型、ラグランジュの方法は追っかけ型と呼ばれたりします。
図のようにある決められた領域の流体の出入りを考えるのが待ち伏せ型のオイラーの方法です。
ラグランジュの方法は流体を1つの小さいかたまりとして見て、そのかたまりを追っかけて運動を考える見方です。
この流体のかたまりを流体素片と言ったりしますが、流体素片は流れとともに形を変えるため、ややこしいことになることもあります。
なので一般的にはオイラーの方法が採用されることが多いですが、ラグランジュの方法のような見方が混ざったような考え方をするケースもありますので、その都度どういう見方をしているのかという点を考えるようにしておきましょう。
流れる量
実用上、単位時間あたりに流体がどれくらいの量が流れたかを知りたいことが多いです。
配管に流れる液体やガスの量だったり、これらがどれだけ流れるのかを管理したりするわけですね。
量を管理したいのに流体の速度だけわかっても困るわけです。
体積流量と質量流量

これらは文字通りの意味ではあるのですが、体積流量はどれくらいの体積の流体が流れているかを示しており、質量流量はどれくらいの質量の流体が流れているかを示しています。
そのまんまですね。
体積流量の単位は\(m^3/sec\)で、質量流量の単位は\(kg/sec\)です。
体積流量については、[ccm]という単位もよく使われたりします。
[ccm]=[cc/min]なので、1分あたり何cc流体が流れたかを示す単位ですね。
[sccm]というのもありますが、s = standardの意味で、1気圧での[ccm]を表すと考えていただければと思います。
流速
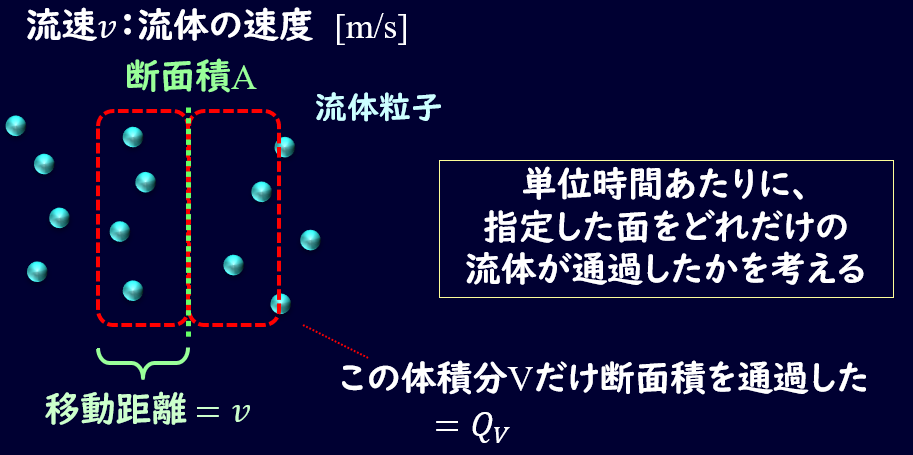
文字通り、流体の流れる速度ですね。
これまでもちょこちょこ出てきていますが、しっかりと定義を把握しておきましょう。
流速は単位時間あたりに、指定した面をどれだけの体積の流体が通過したかを示します。
どれだけの体積の流体が通過したかが大事になってきますので、先ほどの体積流量がポイントになってきます。
それでは、単位時間あたりに面積\(A\)の領域をどれくらいの体積の流体が通過したかを考えましょう。
単位時間あたりに流体が移動する距離は流速\((v\)と同じ値になりますので、体積流量\(Q_v\)は\(Q_v=A×v\)となります。
よって、流速と体積流量には
\[v=\frac{Q_v}{A}\]
という関係が成り立ちます。
この考え方は管を流れる流体を議論する際によく使いますので、しっかりと頭にいれておいていただきたいと思います。
流れ方の種類
それでは、流れ方の分類についてです。
流れを表すには速度が大事な物理量になるわけですが、その速度というのは時間的に変化しうる物理量であり、なおかつベクトル量であることから、時間的な分類と空間的な分類があります。
定常流と非定常流
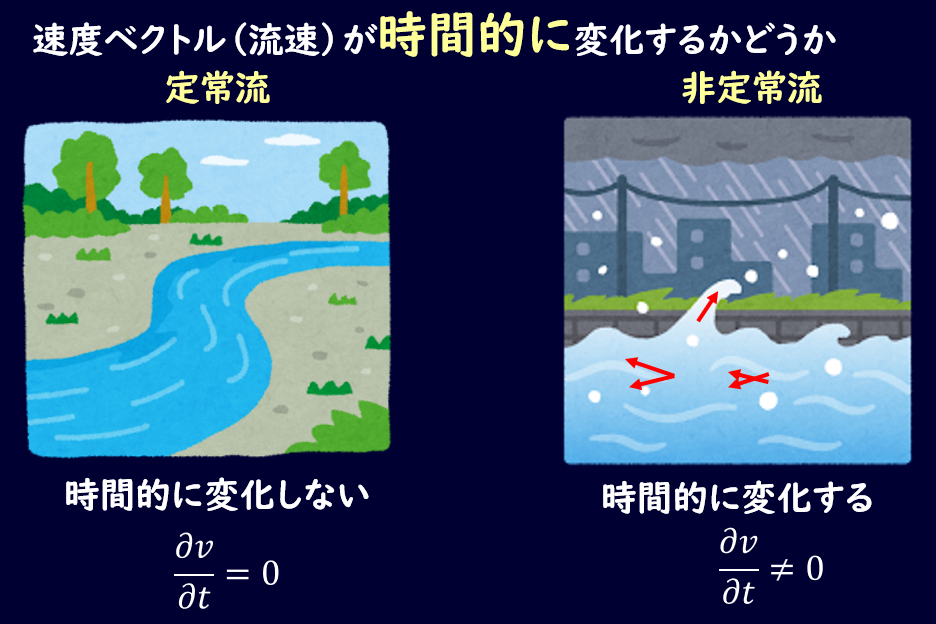
まずは時間的な分類についてです。
流体の速度が時間の関数となっているかどうかを考えるのですが、速度が時間によって変わらない場合=定常流、速度が時間によって変わる場合=非定常流という分類になります。
定常流と非定常流の例は上で示した内容と全く同じで、
定常流は静かな川、非定常流は荒れた川、といったような状態がイメージしやすいのではないでしょうか?
(静かな川というものが厳密な定義なしで使っているので、厳密さに欠けた表現になっていますがざっくりとしたイメージとして捉えていただければと思います。)
これを式で書くと下記のようになります。
流速を\(v\)としたとき、定常流の場合、
\[\frac{\partial v}{\partial t}=0\]
非定常流の場合、
\[\frac{\partial v}{\partial t}≠0\]
速度の時間微分がゼロになるかどうか、という式で表すことができますね。
⚪︎⚪︎次元流れ
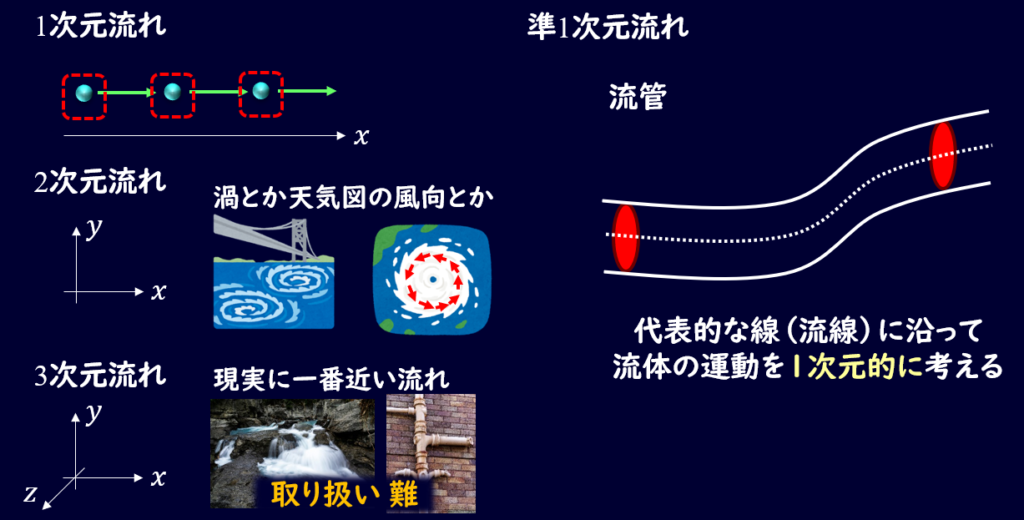
さて、次は空間的な分類についてです。
これは1次元的に考えるか、2次元か、はたまた3次元的に考えるかといった分類で、これもさほど難しい分類ではないと思います。
準一次元流れ
単純な1〜3次元の分類以外にも、準1次元流れという考え方をすることもあります。
1次元から3次元になるにつれて、現象としては複雑になっていき、計算量も多くなっていきます。
この複雑な現象を簡単に考えれるようにするために、準一次元流れというモデルを使うことがあります。
流れについての可視化
流れ方の種類を理解していただいたと思いますが、その流れ方の表し方を示しておきます。
基本的に速度で表すことになるのですが、その速度を可視化してわかりやすくしたり、
流体の速度によって発生している流れの結果、どれくらいの量の流体が流入、流出するのか、を考えたりするので、
実用上、色んな表し方をするということを把握しておきましょう。
メジャーなものは流線、流跡線、流脈線の3つですね。これらを説明していきます。
流線
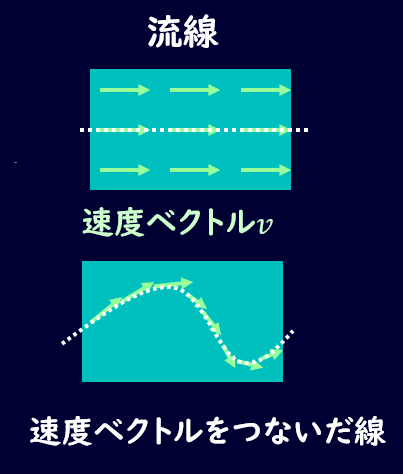
流線はとある時刻での流体の速度ベクトルの接線を繋いだ線です。
長い。説明が。。。
ということで絵で覚えましょう。
流線の特徴としまして、流線同士は基本的に交わらないのですが、『よどみ点』と呼ばれる点では流線が分離したりします。
このよどみ点についてはまた後日記事にさせていただければと思いますので、基本的には交わったりしないんだと思ってもらえればと思います。
流跡線

流跡線はとある流れの中に流体粒子を置いたとき、どういう軌跡で流れていくかを示した線です。
川の中に葉っぱとかを浮かべて、すいーっと葉っぱが動いた軌跡が流跡線に相当しますね。
流脈線

流脈線はよく煙突の煙で例えられます。
とある時刻で、定められた1点を通ってきた流体を線でつなぎ合わせたものになります。
非定常流での流線・流跡線・流脈線
定常流では流線・流跡線・流脈線の3つは一致します。
が、非定常流では下図のように変化します。
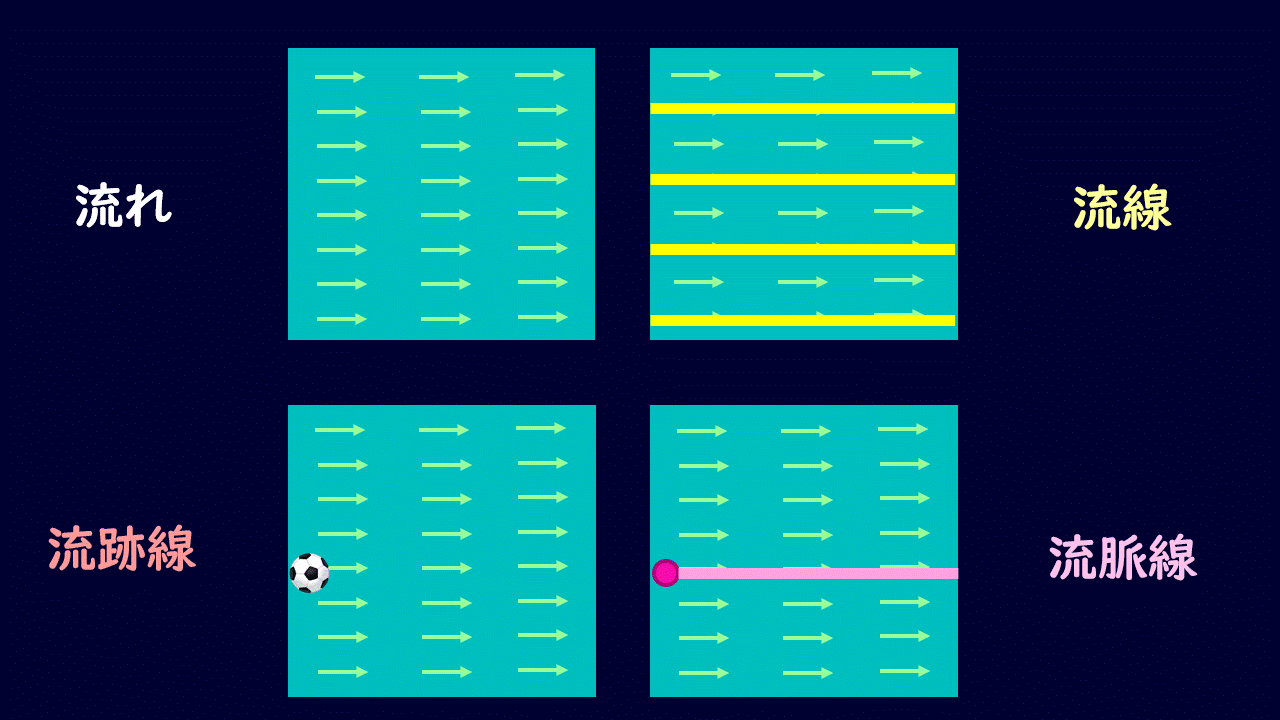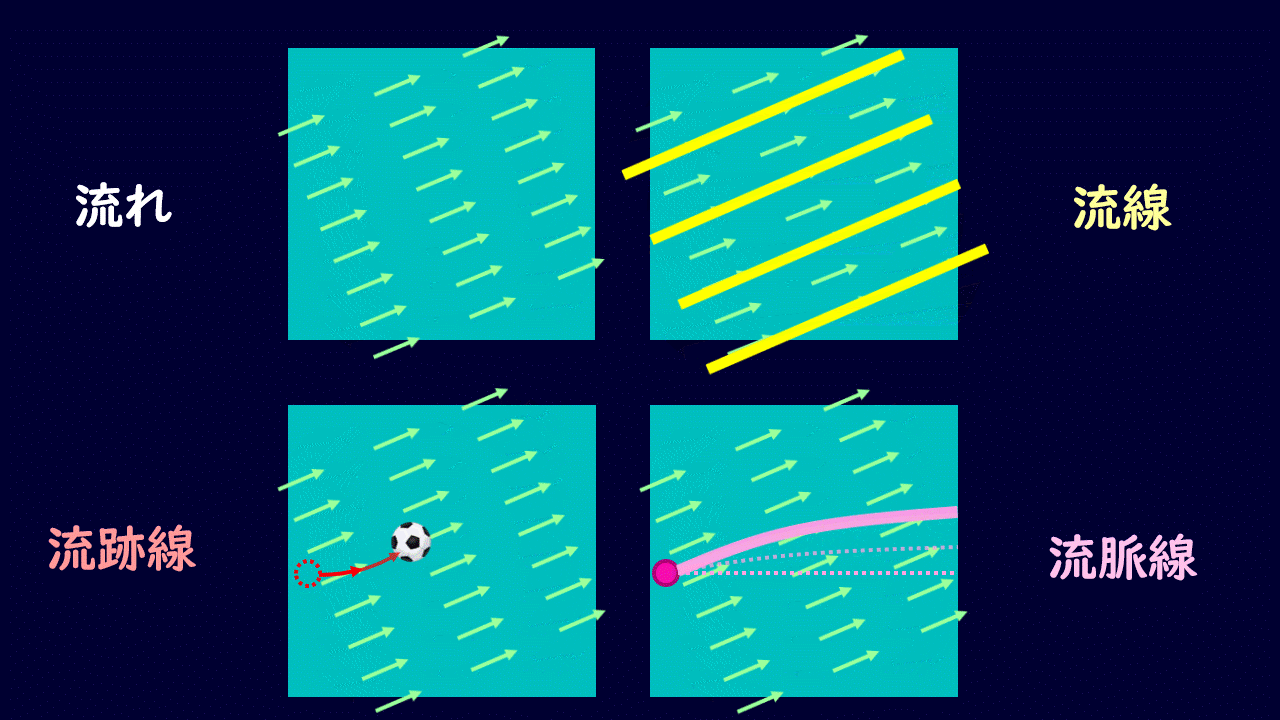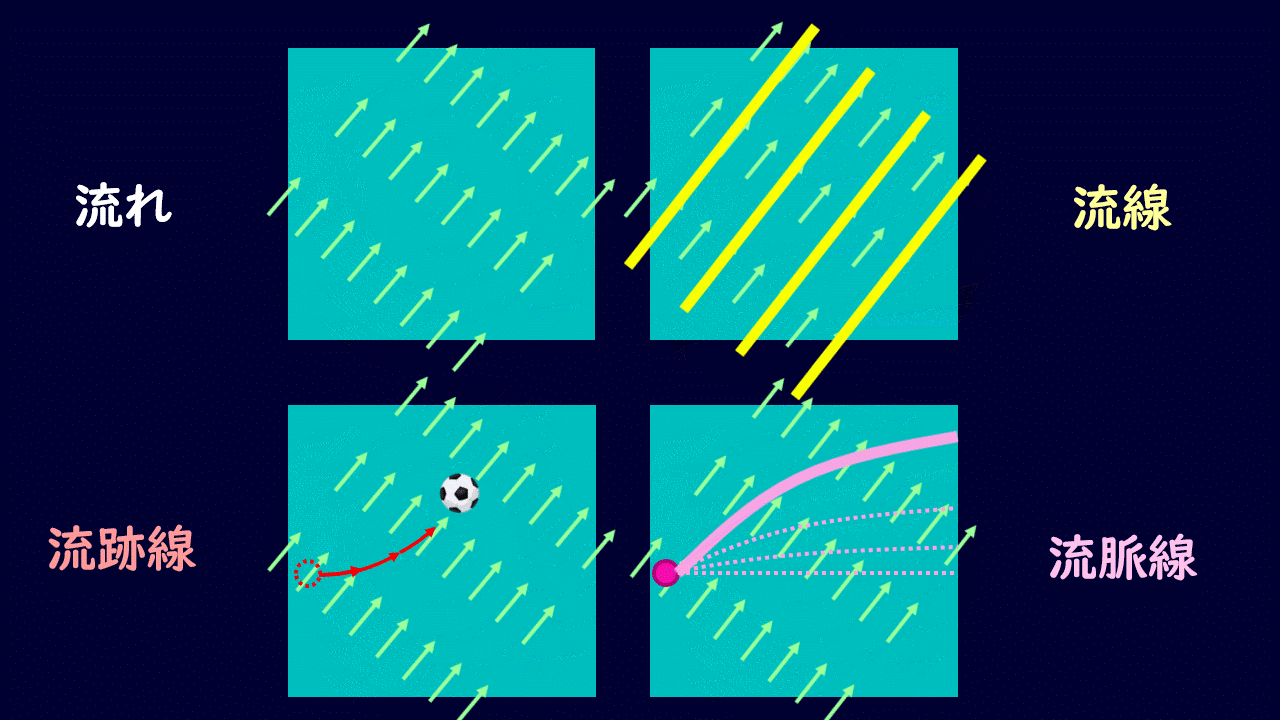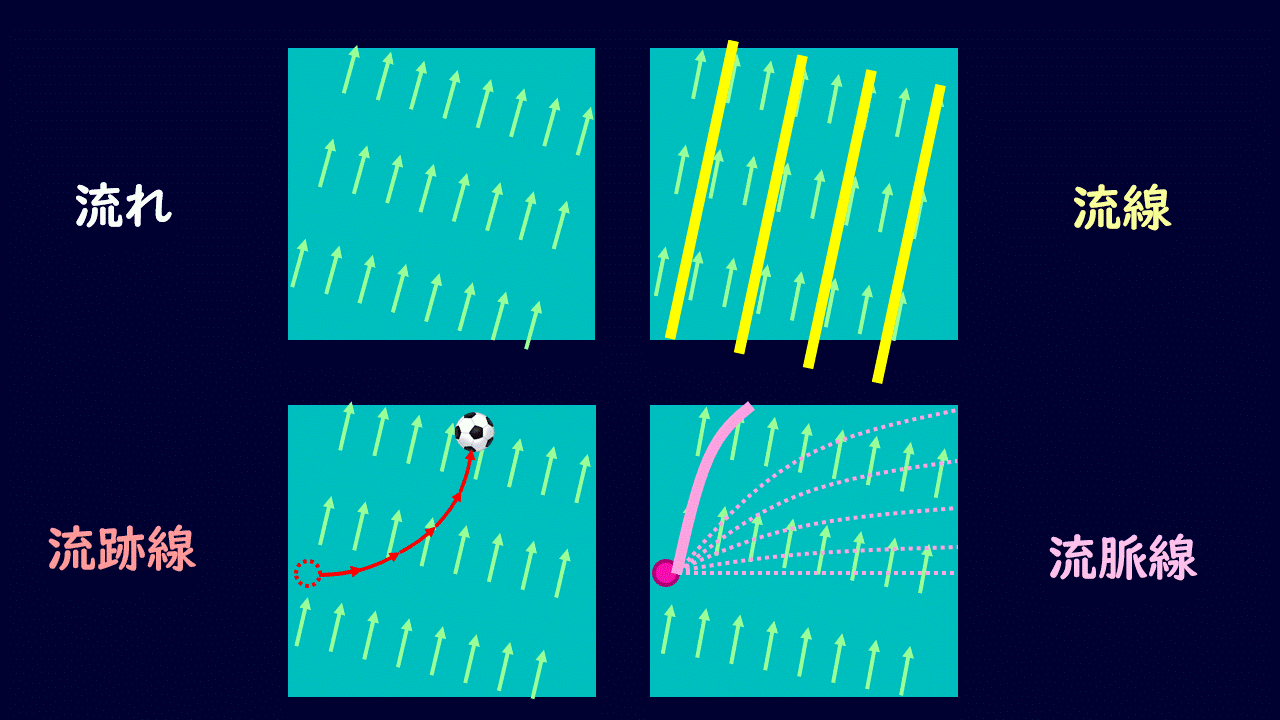
アニメーションのイメージを頭にしっかりと入れておきましょう。
まとめ

流体力学で用いる基礎用語について解説しました。
いずれも今後の流体力学を学ぶ上で基本になるものですので、しっかりと理解しておきましょう。
