曲面にかかる圧力ってどうやって求めたらいいの？
射影した面で考えたらもとまるよ。そのあたりを詳しく解説するね。
今回は曲面にかかる圧力について考えます。
これまで平板にかかる力を考えておりましたが、曲面にかかる圧力がどうなるかを考えましょう。
世の中には曲面に圧力がかかるケースが非常に多く、
潜水艦とか曲面にかかる圧力が大事になってきますね。
曲面にかかる圧力とその方向
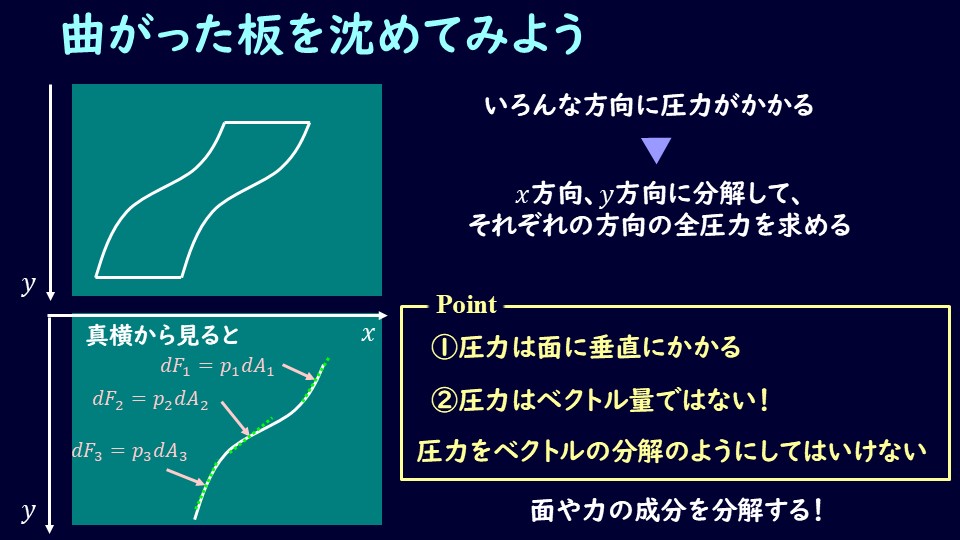
まずどういう方針で考えるかですが、これまでの平板のケースと同様、微小面積を考えていきます。
曲面が水中にあるとして、曲面にかかる水圧を考えていきます。
例えば扇型の弧の部分にかかる圧力を考える時には、弧の部分に微小面積を作ります。
圧力は微小面積に垂直な方向にかかりますので、図のようになりますね。
全圧力は弧全体の力を積分して足し合わせればよいので、各方向を考えればよいことになります。
これを\(x\)軸、\(y\)軸にわけて書くとこのようになりますね。
分けて書くとそれぞれ\(x\)軸、\(y\)軸の方向に投影面を作るのと同じです。
ちなみに圧力そのものを各方向に分解してはいけません。
厳密にはテンソル量と呼ばれますが、ベクトルのように分解できる量ではないのです。
どちらかというとスカラー量に近い位置付けで、テンソルとかにアレルギーある方は、最初のうちはスカラー量とみなしてもらって構いません。
ちなみに力はベクトル量なので図形的に分解してもオッケーです。
さて、このような考えのもと、\(x\)軸方向と\(y\)軸方向の微小面積にかかる力を考えましょう。
θの角度で傾いている微小面積\(dA_1\)を考えると、\(x\)方向の面\(dA_x\)にかかる力\(dF_x\)は
\[dF_x=pdA_x=pdA_1cosθ_1\]
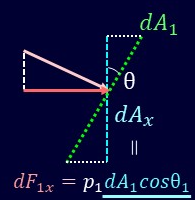
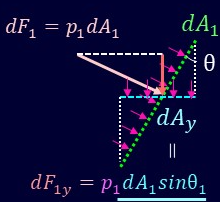
となり、同様に\(y\)方向も微小面積\(dA_y\)、力を\(dF_y\)とすると、
\[dF_y=pdA_y=pdA_1sinθ_1\]
となりますね。
各方向の全圧力は積分すれば良いので、\(x\)方向は
\[F_x=\int dF_x=\int pdA_x\]
圧力\(p=ρgy\)なので、
\[F_x=\int ρgydA_x\]
これは、過去の記事でも解説した、平板を水中に沈めたときの全圧力と全く同じ状態ですね。
平板の場合の全圧力の式は、図心の圧力×全面積で表すことができて、図心の位置を\(\bar{y}\)とすると、
\[F_x=ρg\bar{y}×A_x\]
と書くことができます。
\(y\)方向は
\[F_y=\int dF_y=\int pdA_y\]
これは物理的な意味を少し考えてみましょう。
この式は鉛直方向にかかっている力の総和を表しているのですが、この力の起源はなんでしょう？
水圧を考えているわけですが、そもそも水圧は圧力がかかっている面の上側にある流体の重力によるものでした。
今回のケースも同様で、\(y\)方向の式は、考えている面の上側にある流体の重力を示しています。
その体積をVとすると、
\[F_y=ρgV\]
となります。
これで全圧力の\(x\)方向と\(y\)方向の成分が求まりましたので、その全圧力は
\[F=\sqrt{F_x^2+F_y^2}=ρg\sqrt{(\bar{y}A_x)^2+V^2}\]
となります。
また、全圧力の向きαは
\[α=tan^{-1}\frac{F_y}{F_x}\]
と表すことができます。
まぁ手計算でパッと求まるようなものではないので、素直に関数電卓とかで計算してあげましょう。
まとめ
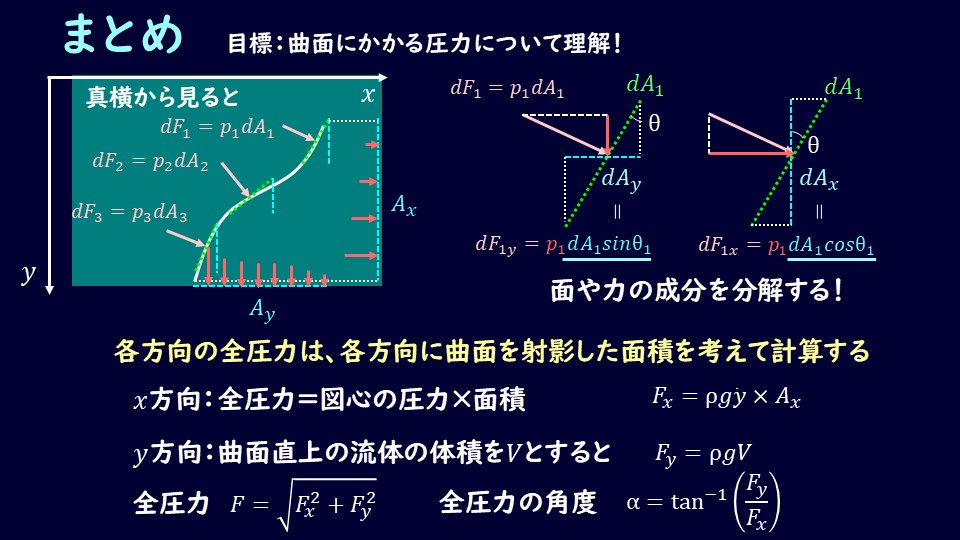
曲面に作用する全圧力とその向きを解説しました。
各軸方向の投影面で考えることがとても大事ですので、図形的なイメージをしっかりと持てるようにしていただければと思います。