壁面にかかる圧力なんて簡単だよー…ってあれ?圧力中心?図心?なんじゃこりゃ?


この辺りは高校物理では習わないからね。大学レベルにしっかりアップデートしていこう。
今回から大学レベルへのアップデートが始まります。
もう少し進むと、実は材料力学で学んだ断面1次モーメントとか断面2次モーメントとかが出てきます。
まだ習って無い人ごめんなさい。材料力学の復習も兼ねて勉強していきましょう!
動画でも解説しておりますので、そちらも参考にしていただければと思います。
壁面にかかる圧力
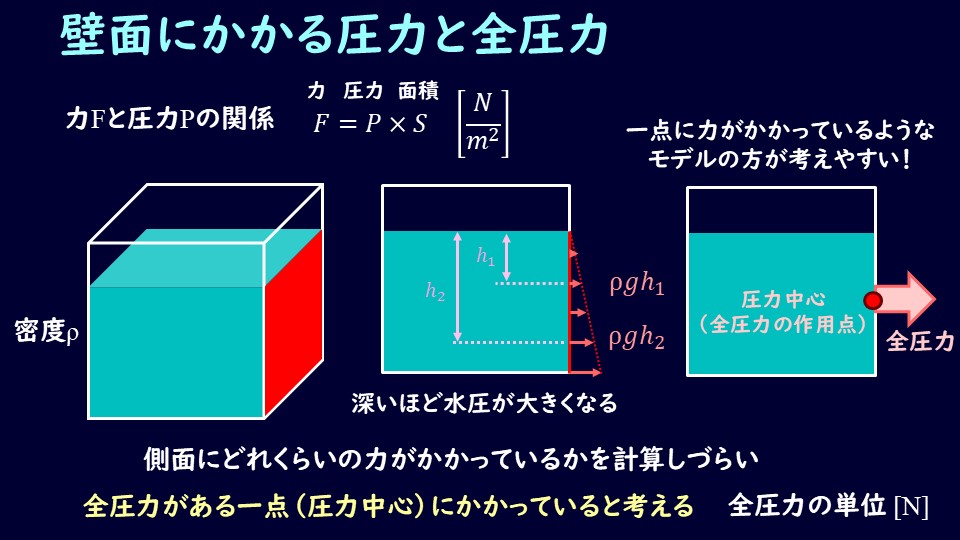
水槽があって、壁にかかる圧力を考えてみましょう。
これだけならそんなに難しくないですね。
前々回の水圧の内容で対応できます。
水圧の式は、ゲージ圧力だと
\[P=ρgh\tag{1}\]
ですね。
圧力は等方的にかかるので、壁に垂直に圧力がかかるとすれば、その大きさはその深さの水圧に等しくなります。
よって、深くなるほど直線的に壁にかかる圧力は大きくなりますね。
壁にかかる力(全圧力)
さて、それでは壁にはトータルでどれくらいの力がかかっているでしょう?
さらにはその力はどの場所にかかっているでしょう?
圧力ではなく、Totalの力がどうなっていて、作用点がどこにあるか、を求めるというのは力学全般で大事な視点ですね。
壁は質点ではなく、連続体、つまり点ではなく大きさをもつ物体なので、つり合いを考える時には力とモーメントを考える必要があり、圧力による力とその作用点を考えることは非常に大事になります。
この圧力による圧力のトータルした力を全圧力と呼びます。
圧力という名前がついていますが、全圧力の単位はNで力と同じ次元になり、圧力とは単位が異なるので注意しましょう。
全圧力の単位は力と同じ[N]です。ややこしい…
で、この全圧力がかかる点を圧力中心と呼びます。圧力中心を求めるのは少しややこしいので、詳細は次の記事で説明しようと思います。
まずは簡単な例題で全圧力を求めていきましょう。
最初は空気内に板を置いてみましょう。

板の面内に一様に圧力がかかることになりますね。
板の面積をA、圧力(気圧)をpとすると、全圧力Fは
\[F=pA\tag{2}\]
となりますね。これは非常に簡単。
次に単純な壁です。水族館の水槽をイメージしてもらえればと思います。
壁にかかる圧力の分布を考えてみると、水圧は深くなるほど1次関数的に大きくなるので、図を書くと下図のような形になりますね。
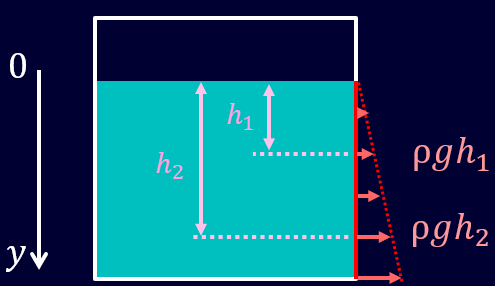
水圧がかかっている面の面積を\(A\)、\(y\)軸を下向きにとって、水面をゼロとすると、
\[p=ρgy\tag{3}\]
全圧力\(F\)はこの面にかかっている力なので、これを全ての面で積分してあげればよいので、
\[F=\int pdA=\int^b_0\int^h_0pdxdy\tag{4}\]
このようになります。
多重積分となっているのでうぇ~ってなっているかもしれませんが、それほど難しくないです。
\(p\)を式に代入して計算してみると
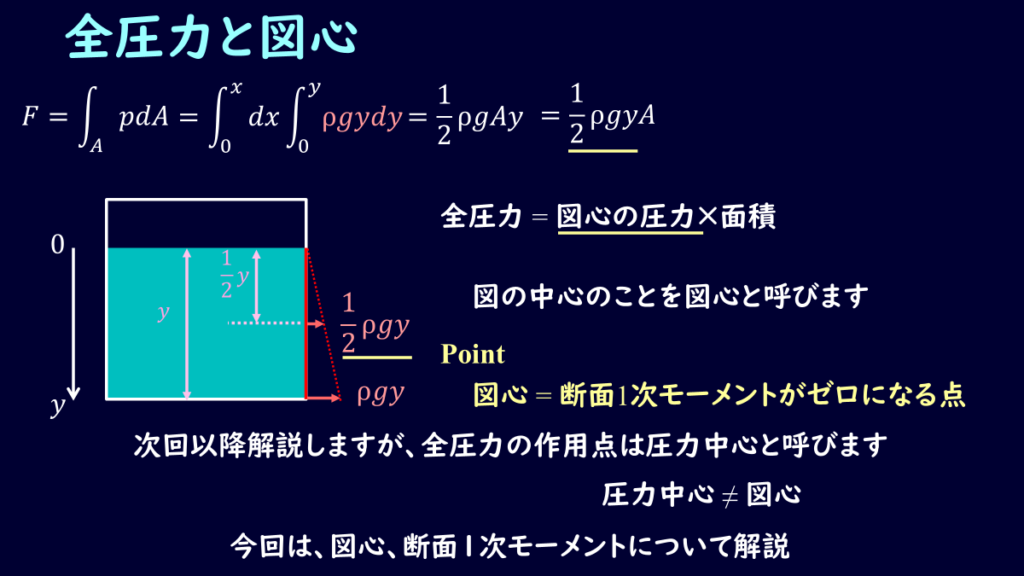
\[F=\int^b_0dx\int^h_0ρgydy=ρgx・\frac{1}{2}y^2=\frac{ρgy}{2}・A\tag{5}\]
ちなみに全圧力の作用点である圧力中心は、板の中央で\(\frac{y}{2}\)となります。
上の式は『全圧力=板の中央にかかる水圧×面積』となっていることがわかりますね。
全圧力の公式
さて、ここまでは手計算で楽々解ける内容でしたが、複雑な問題だとそうはいきません。
全圧力には公式があり、覚えておくと計算量をグッと抑えられるので、理解しておきましょう。
単一流体の中では次の公式が成り立ちます。
\[F=p(y)A\tag{6}\]
ここで\(y\)は図心の位置で、\(p(y)\)は図心の位置での圧力です。
この式は覚えておくことをおすすめしますが、内容の理解も大事ですので、深掘りしていきますね。
図心と重心の違い
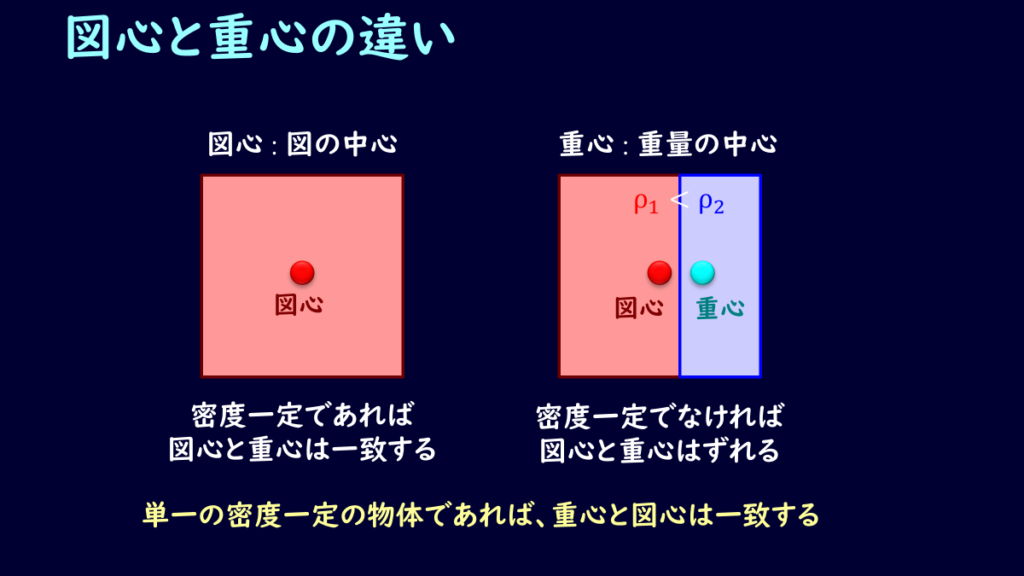
さて、図心という文言が出てきましたが、断面1次モーメントと合わせて理解していきましょう。
図心とは文字通り、図の中心のことです。
似たようなもので重心というものがありますが、内容は少し異なりますので、違うものという認識を持っておいてください。
まずは重心と図心の違いについて解説しましょう。
重心はメジャーな単語なので、直感的に理解している人も多いかもしれませんが、
『重力によるモーメントがゼロになる点』
と言うことができます。
一方、図心は密度とか重さとかは関係なく、その図の形の中心を示します。
この図心を求めるのに必要なのが断面1次モーメントで、図心を通る軸からの断面1次モーメントはゼロになります。
\[\int ydA=0\tag{7}\]
断面1次モーメントはこの式の左辺のことなのですが、断面1次モーメントってなんやねん!という方もいらっしゃると思いますので、解説しますね。
脱線に脱線を重ねていますがご容赦ください…
断面1次モーメント

さて、モーメントという名前がついておりますが、まずモーメントとは?というところに立ち返ると、モーメントは次のようなものになります。
モーメント=⚪︎⚪︎×距離
⚪︎⚪︎のところに力を入れると、高校でも習う力のモーメントになりますし、運動量を入れると角運動量モーメントになります。
断面1次モーメントは先ほど説明に出てきたとおり、下記ですね。
\[\int ydA\tag{8}\]
\(y\)はとある点や軸からの距離をしめします。
でも、全圧力のところと繋がっているように見えないんだけど…


それじゃあここまでで基礎知識を理解できたと思うので、全圧力、図心、断面1次モーメントをつなぎ合わせていこう。
お待たせしました。
全圧力の公式、\(F=p(y)A\)を導いていきましょう。
とはいえ、少し前で説明した重心の考え方を使った方が理解しやすいと思うので、重心について少し深掘りします。
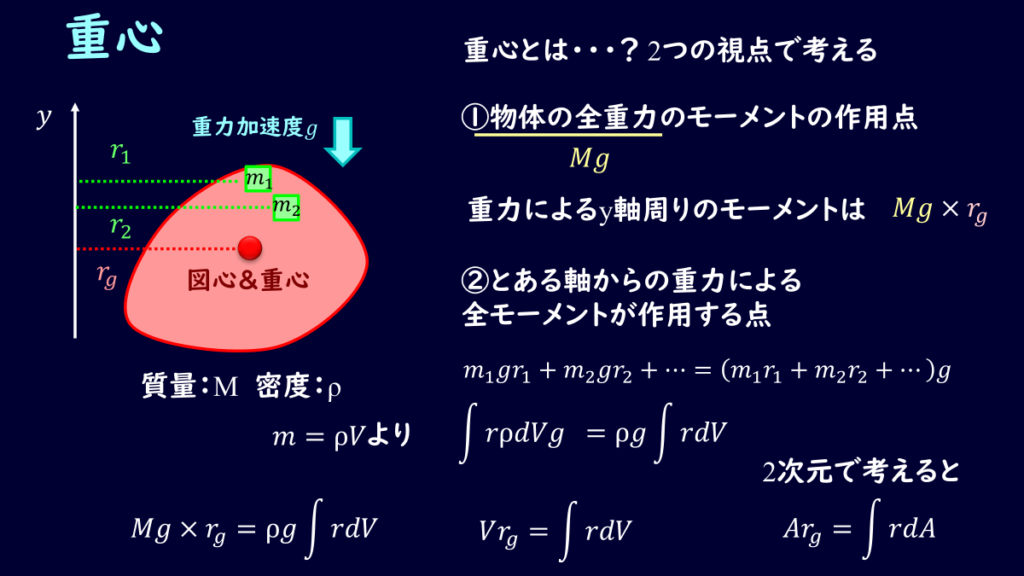
さて、とある剛体を静止させようとすると、力のつり合いとモーメントのつり合いを考える必要がありますね。
重心は先ほど示したたとおり、
『重力によるモーメントがゼロになる点』
であって、この点を下から支えると回転することなく支えることができます。
言い換えると、『全重力の作用点』とも言えます。
重心以外の点で支えると、重力によるモーメントが発生してぐるっと回ってしまうわけですね。
で、剛体の質量である\(M\)、重力加速度を\(g\)とすると、\(Mg\)の力が重心にかかるので、
重心を\(Mg\)の力で支えると力もモーメントもつり合って、剛体は静止することになります。
つまり、剛体に発生する重力は重心に\(Mg\)となるので、次の式のように書くことができます。
\[Mg=\sum m_ig\tag{9}\]
\(m_i\)は剛体を細かく分割したときの、i番目の質量を指します。
これを微小体積にまで細かく分割すると、
\[Mg=\int ρdVg\tag{10}\]
となります。
密度\(ρ\)と微小体積\(dV\)を掛け合わせると微小体積の質量\(m\)になりますね。
さて、これは重力を積分した結果なので、次にとある位置からの重力によるモーメントを考えてみましょう。
考え方は重力の時と同じです。
微小体積のモーメントを考えて積分することになり、
\[\int rρdVg\tag{11}\]
となります。
これが積分することによって求まる重力によるモーメントの計算ですが、
ここで別の視点を入れます。
重力によるモーメントを考えたとき、全重力で代表させたとき、重心が作用点である、とみなすことができますので、
\[\int rρdVg=Mgr_g\tag{12}\]
と書けます。ここで重心までの距離を\(r_g\)としています。この式を整理すると
\[ρg\int r dV=Mgr_g\tag{13}\]
両辺を\(ρg\)で割ると
\[\int r dV=Vr_g\tag{14}\]
\(M\)を密度\(ρ\)で割ると体積\(V\)になりますね。
この式を見てみると、微小体積のモーメントは全体積×重心までの距離
という形になっていますね。
これは3次元で考えているのでこうなりますが、次元を落として2次元で考えても同様です。
つまり、
\[\int r dA=Ar_g\tag{15}\]
となって、断面1次モーメントは全面積×重心までの距離
となります。
密度が一定なら重心と図心の位置は一致するので、
断面1次モーメントは全面積×図心までの距離
となります。
全圧力と断面1次モーメントの関係
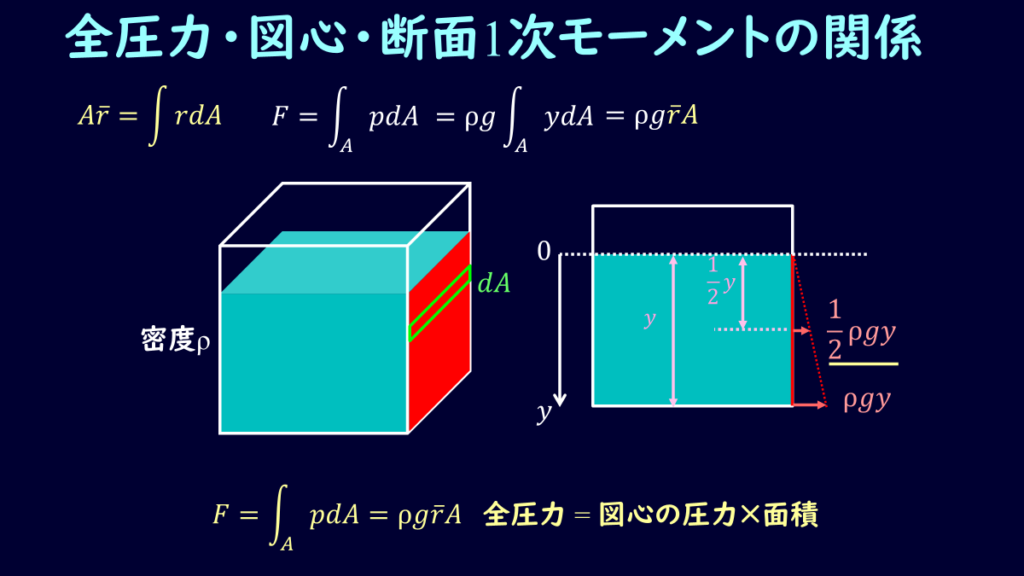
このように、図心と断面1次モーメントの関係性がわかったところで、全圧力の式との関係性を見てみましょう。
全圧力の式は
\[F=\int pdA=ρg\int ydA\tag{16}\]
という形でしたね。
断面1次モーメントは(15)式を使って表すことができるので、図心の座標を\(\bar{r}\)とすると、
\[F=ρg\bar{r}A\tag{17}\]
となり、『全圧力=図心の圧力×面積』 という式になりますね。
このように全圧力の式は図心の圧力を使って表すことができるわけです。
この式を使うと、いろんな問題を解きやすくなりますので、しっかりと頭に入れておきましょう。
練習問題 斜めの板を沈めた場合
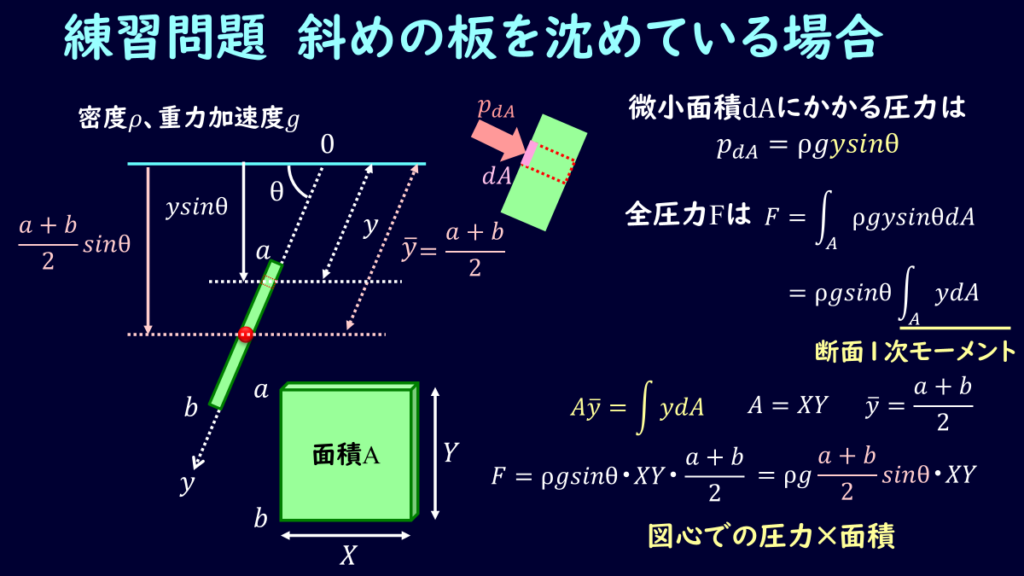
前提として、下図のように水槽に沈めた板の水圧を考えましょう。
まず、軸を図のようにとります。
板はθだけ傾いているとして、傾いている方向に軸の方向をとります。
このように軸をとると、とあるy座標での深さは\(ysinθ\)となりますね。
なのでとあるy座標における微小面積の圧力は、
\[p_{da}=ρgysinθ\tag{18}\]
全圧力\(F\)は
\[F=\int_AρgysinθdA=ρgsinθ\int_AydA\tag{19}\]
断面1次モーメントは先ほど示した通り、図心の座標×面積なので、板の横と縦の長さを\(X、Y\)とし板の上部と下部の\(y\)座標を\(a、b\)とすると、
\[F=ρgsinθXY\frac{a+b}{2}=ρg\frac{a+b}{2}sinθ・XY\tag{20}\]
と書くことができます。
斜めの板の場合でも図心での圧力×面積となっていることがわかると思います。
まとめ

全圧力と断面1次モーメントについて解説しました。
斜めに沈めても、平板の形状が変わっても、全圧力は図心の圧力×面積となることをしっかりと理解しておきましょう。
