流体力学の中でも、高校物理でも習う内容について復習します。
とはいっても、止まっている流体についての話なので、流体静力学とも言ったりする分野になります。
復習する内容は、圧力・水圧(気圧)・浮力の3つです。
特に圧力・水圧に関しては、赤ちゃんが歩く前のハイハイくらいの基礎みたいなものです。
今後の流体力学の学習における基礎の基礎とも言える内容ですので、しっかりと理解しておきましょう。
YouTubeでも解説しておりますので、ぜひ参考にしていただければと思います。
圧力について
圧力の定義とイメージ
圧力の定義を確認しておきましょう。
『こいつなにもんや!』っていうのを知っておくのは何をするにしても重要ですので。
圧力は『単位面積にかかっている力』のことで、単位は\(N/m^2\)です。
式的には力\(F\)、面積\(S\)、圧力を\(P\)とすると、
\(P=F/S\)
まぁ日常生活でも使うこともあるのではないでしょうか?
例えば、革靴とかスニーカーの人に踏まれたら痛いですが、ハイヒールの細いところで踏まれたら骨折するとかあったりするんですね。
これは同じ60kgの人に踏まれたとしても、圧力は面積が小さいほど大きくなってしまうからなんですね。
一点集中されると痛いのです…注射と同じ。花火大会とか満員電車では気をつけてくださいね。
圧力の性質
圧力の大事な性質を押さえておきましょう。
圧力の性質
①圧力の等方性
②圧力は面に垂直にかかる
③押し込まれたときの圧力は流体内のどこでも同じ(パスカルの原理)
①と②については、圧力の方向についての話ですね。
①は質点を水の中に沈めたケースをイメージしてほしいのですが、質点全体に等方的にかかります。なんか変な向きにだけ強くなったりしないよーっていうことです。
まぁそんなことあったら気持ち悪いですよね。
学校のプールに入って、
『なんか左手だけ水圧でつぶされそうなんですけどー!』
みたいなことって、すっごいレアなケース考えない限りないと思うんです。
そんなプールを持つ学校は入学やめたり転校したほうがいいです。
で、そんな圧力(水圧)ですが、単位面積当たりの力なので、どこかの面を指定してあげる必要があります。
その指定した面に対して垂直な向きの方向が圧力がかかる向きです。
最後のパスカルの原理は、イメージとしては満員電車のイメージです。
満員電車に無理やり人を押し込んだ時に、電車の中にいる人には均等に力がかかります。
押し込まれた人が、周りの人を押して、その押された周りの人が、また周りの人を押して…
といった感じで、力が伝搬していくイメージです。
これを利用したのが油圧ジャッキと呼ばれる道具ですね。一家に一台、油圧ジャッキ。
もしかしたら倉庫に眠っていて知らない方もいらっしゃるかもしれませんが、重たいものを軽い力で持ち上げるものですね。
次の記事で油圧ジャッキの問題を解説予定ですので、楽しみにしておいてください。
水圧(気圧)について
水圧(気圧)は、水や空気など、流体中にいたときに受ける圧力のことですね。
天気予報とかでも高気圧、低気圧とか言ってたりすると思いますが、あれは大気中の圧力を言っているわけですね。
気圧が低いほうに空気が流れていくので、低気圧のところに雲ができやすかったり、気圧が非常に低いと台風となって災害につながります。
水圧についても、水の中を深く潜っていくと、水圧でペシャンコになっちゃうって聞いたことがあると思います。
実際に、潜水艦が深海の水圧に耐え切れなくなって、つぶれてしまった事故が起こったりしていますね。恐ろしい…
水圧に耐えきれる設計ができていないと、大惨事になります。
上記の潜水艦もそうですし、水族館とかもそうですね。急に水族館のアクリルが割れたらパニック間違いなしですよね。
というわけで、これらの圧力がどのようにかかるのかを知るということは、安全の面でも非常に大事なことになってくるわけです。
水圧の式
その大事な水圧については高校物理でも習い、いろんな問題があります。
まずは水圧の式を理解しましょう。
質点にかかる水圧を\(P\)、水(流体)の密度を\(ρ\)、重力加速度\(g\)、質点の水面からの深さを\(h\)とすると
\(P=ρgh\)
となります。大気圧は無視してます。
水面からの高さ\(h\)が入っていますので、深い位置では水圧が大きくなることが理解できると思います。
これは質点の直上にある水の重力の総和として考えることができます。
横方向にかかる水圧は、すぐ横の流体がその直上の流体による水圧(重力)をパスカルの原理によって押し込まれたため発生すると解釈できます。
気圧でも同じことが言えて、山の山頂に近づくほど気圧が下がります。
これは気圧が0になる位置を基準とし、そこからの深さが山頂のほうが浅くなるため、気圧が下がるのですね。
気圧が下がると、ポテチの袋がパンパンになっていたり、水の沸騰する温度が下がったりします。
私も富士山に登ったことがありますが、山頂でのみそラーメンはぬるいサッポロ一番の味がしました。それでもおいしかったです。
水圧の練習問題は流体力学シリーズの最初のほうでたくさんやりますので、そこで使い方を慣れていきましょう。
今は水圧の式をしっかりと覚えておいてくださいね。
ゲージ圧力と絶対圧力
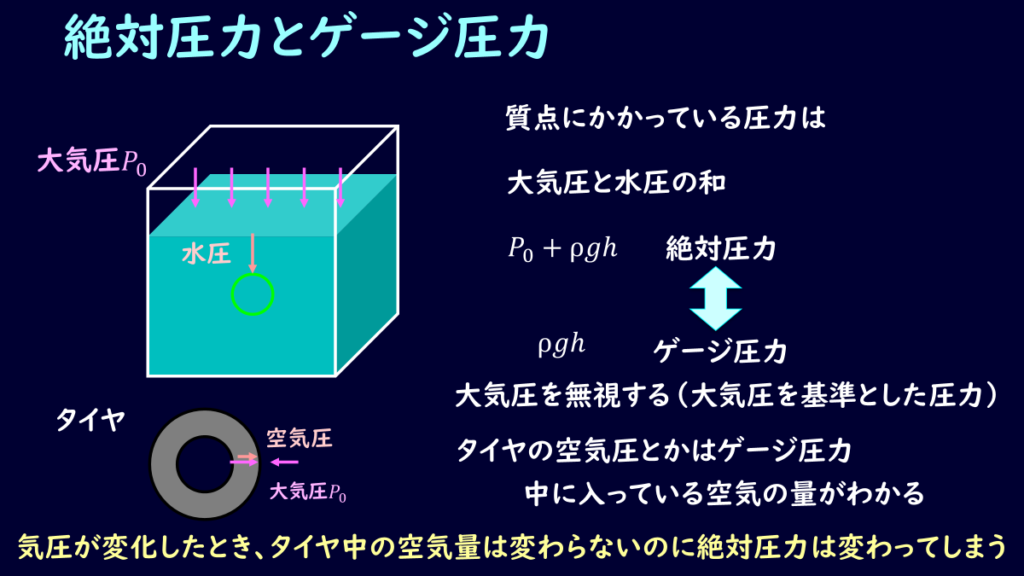
上記の水圧の式については、実はゲージ圧力と呼ばれる表記の仕方になります。
圧力の表記の仕方については、ゲージ圧力と絶対圧力の2種類があり、使い分けがされています。
ゲージ圧力は大気圧を基準にしたときの圧力で、絶対圧力は大気圧も込みでの圧力となります。
つまり、先ほどの水圧の式では、
ゲージ圧力:\(P_0+ρgh\)
絶対圧力:\(ρgh\)
\(P_0\)は大気圧です。
ゲージ圧力で表記されている例としては、タイヤの空気圧などです。
タイヤの空気圧で何を見ているかというと、タイヤの中にどの程度の空気が入っているかを見ています。
気圧が変化したときに、タイヤの中の空気量は変わらないのに絶対圧力が変わってしまいます。
浮力

これを水の中にいれると浮かびますか?沈みますか?っていうのはクイズで鉄板の問題でありますよね。
個別に浮かぶか沈むかっていうのを覚えておくのは大事なことではありますが、なぜ浮かぶのかを理解することのほうがとても大事なので、理屈をしっかりと把握しておきましょう。
アルキメデスの原理から浮力の式が出てきます。
アルキメデスさんはお風呂に入ったときにあふれ出したお湯を見て、原理に気づいて興奮のあまり裸で町中を走り回ったヤンチャなお方ですが、正直よく気付いたなって思いますね。
水圧を考えるときに質点で考えていましたが、質点ではなく、連続体(なんか形があるもの)として考えたときに、浮力が現れます。
この浮力が物体にかかる重力より大きい場合、浮かぶことになります。
船を浮かべるとかにおいて大事な考え方になりますので、浮力についてもしっかりと理解しておきましょう。
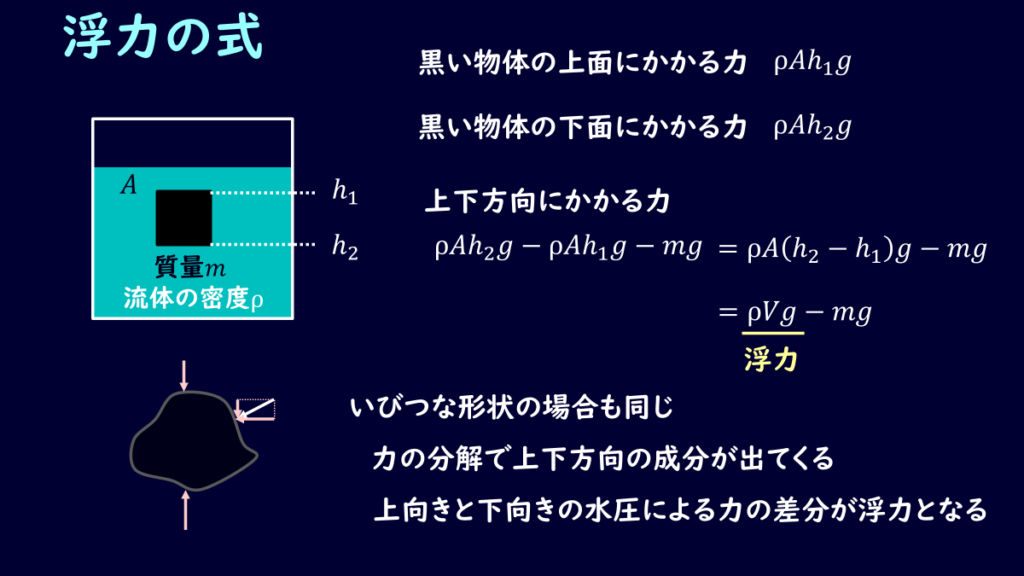
高校物理で学ぶ浮力の公式は以下のようになりますね。
\(f=ρVg\)
\(ρ\)は流体の密度ですので間違わないように。
浮力は押しのけた流体の分だけ発生する、と習った方も多いのではないでしょうか。
公式丸覚えでもよいのですが、なぜこの式になるかを理解しておきましょう。
先程もちらっと出ましたが、浮力は質点系ではなく、連続体のときに現れる力のです。
図のように高さのある直方体を水の中に沈めます。
すると流体中なので、水圧が発生するのですが、直方体の上面と下面で水圧の大きさが変わってきます。
それぞれの水圧の大きさを計算してみると、上面の水面からの深さを\(h_1\)、下面の深さを\(h_2\)として、
上面 \(ρAh_1g\)
下面 \(ρAh_2g\)
差を取ると、\(ρA(h_2-h_1)g\)
ここで直方体の体積が\(A(h_2-h_1)g\)なので、\(V\)とすると上式は
\(ρVg\)
になりますね。
これは簡単な直方体の場合ですが、複雑な形状の場合は上面にかかる力と下面にかかる力を積分して求めてあげれば良いですね。
複雑な形状にかかる水圧ついては、曲面にかかる水圧についての理解を深めてからの方がよいと思いますので、また後日記事にさせていただければと思います。
まとめ
高校物理で習う圧力・水圧(気圧)・浮力について復習しました。積分を使って一般化することができれば、より深い理解ができると思います。まずは流体力学の基礎知識としてしっかりと覚えておきましょう。何事も基礎が大事です。
